
【题目】如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.
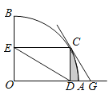
(1)求证:∠CGO=∠CDE;
(2)若∠CGD=60°,求图中阴影部分的面积.
【答案】(1)见解析;(2)图中阴影部分的面积为![]() .
.
【解析】
(1)连接OC交DE于F,根据矩形的判定定理证出四边形CEOD是矩形,根据矩形的性质和等边对等角证出∠FCD=∠CDF,然后根据切线的性质可得∠OCG=90°,然后根据同角的余角相等即可证出结论;
(2)根据题意,求出∠COD=30°,然后利用锐角三角函数求出CD和OD,然后根据扇形的面积公式和三角形的面积公式即可求出结论.
证明:(1)连接OC交DE于F,
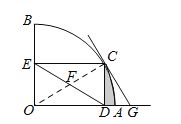
∵CD⊥OA,CE⊥OB,
∴∠CEO=∠AOB=∠CDO=90°,
∴四边形CEOD是矩形,
∴CF=DF=EF=OF,∠ECD=90°,
∴∠FCD=∠CDF,∠ECF+∠FCD=90°,
∵CG是⊙O的切线,
∴∠OCG=90°,
∴∠OCD+∠GCD=90°,
∴∠ECF=∠GCD,
∵∠DCG+∠CGD=90°,
∴∠FCD=∠CGD,
∴∠CGO=∠CDE;
(2)由(1)知,∠CGD=∠CDE=60°,
∴∠DCO=60°,
∴∠COD=30°,
∵OC=OA=4,
∴CD=2,OD=2![]() ,
,
∴图中阴影部分的面积=![]() ﹣
﹣![]() 2×2
2×2![]() =
=![]() π﹣2
π﹣2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论:![]() ;
;![]() >0;(3)若点
>0;(3)若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
;![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.
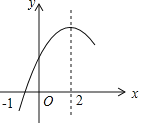
查看答案和解析>>
科目:初中数学 来源: 题型:
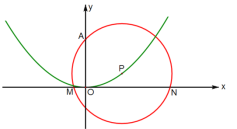
【题目】如图,抛物线y=ax2+bx+c(a、b、c是常数,a≠0)经过原点O和![]() 两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).
两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0, 2).
(1)a= ,b= ,c= ;
(2)求证:在点P运动的过程中,⊙P始终与x轴相交;
(3)设⊙P与x轴相交于M、N两点,M在N的左边.当△AMN为等腰三角形时,直接写出圆心P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】像![]() =x这样的方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,当x1=3时,
=x这样的方程,可以通过方程两边平方把它转化为2x+3=x2,解得x1=3,x2=﹣1.但由于两边平方,可能产生增根,所以需要检验,经检验,当x1=3时,![]() =3满足题意;当x2=﹣1时,
=3满足题意;当x2=﹣1时,![]() =﹣1不符合题意;所以原方程的解是x=3.运用以上经验,则方程x+
=﹣1不符合题意;所以原方程的解是x=3.运用以上经验,则方程x+![]() =1的解为_____.
=1的解为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
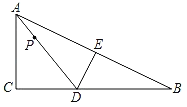
【题目】如图,在△ABC中,∠C=90°,AC=8,BC=16,点D在边BC上,沿DE将△ABC折叠,使点B与点A重合,连接AD,点P在线段AD上,当点P到△ABC的直角边距离等于5时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年学校举行足球联赛,共赛17轮(即每队均需参赛17场),记分办法是:胜1场得3分,平1场得1分,负1场得0分.在这次足球比赛中,小虎足球队得16分,且踢平场数是所负场数的整数倍,则小虎足球队所负场数的情况有( )
A.2种B.3种C.4种D.5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 在边
在边![]() 上,连接
上,连接![]() .
.
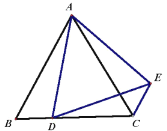
(1)如图1,求证:![]() ;
;
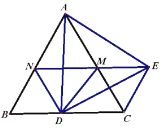
(2)如图2,点![]() 在
在![]() 上,
上,![]() (
(![]() ),连接
),连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中所有与线段
,在不添加任何辅助线的情况下,请直接写出图2中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
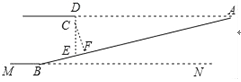
【题目】为缓解交通压力,市郊某地正在修建地铁站,拟同步修建地下停车库.如图是停车库坡道入口的设计图,其中MN是水平线,MN∥AD,AD⊥DE,CF⊥AB,垂足分别为D,F,坡道AB的坡度=1:3,AD=9米,点C在DE上,CD=0.5米,CD是限高标志牌的高度(标志牌上写有:限高 米).如果进入该车库车辆的高度不能超过线段CF的长,则该停车库限高多少米?(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈3.16)
≈3.16)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com