
 某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.)
某研究性学习小组,为了测量某池塘边A、B两点间的距离,让一架航模在直线AB的正上方24米的高度飞行,当航模位于点D处时,在A点处测得航模仰角为60°,5分钟后,当航模在点C处时,在B点测得航模仰角为45°,己知航模飞行的速度为每分钟45米,试计算A、B两点的距离.(结果精确到0.1米,参考数据:$\sqrt{2}=1.41,\sqrt{3}$=1.73.) 分析 作DM⊥AB于M,BN⊥CD于N,则DM=BN=24米,在Rt△ADM中,由题意∠DAM=60°,故可得出AM的长,同理可得出CN的长,根据AB=AM+MB即可得出结论.
解答 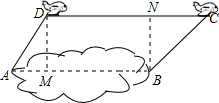 解:如图所示,作DM⊥AB于M,BN⊥CD于N,则DM=BN=24米,
解:如图所示,作DM⊥AB于M,BN⊥CD于N,则DM=BN=24米,
在Rt△ADM中,由题意∠DAM=60°,
∴AM=$\frac{24}{tan60°}$=8$\sqrt{3}$米,
在Rt△BNC中,由题意∠NCB=45°,
∴DN=DC-NC=45×5-24=201米,
∴AB=AM+MB=8$\sqrt{3}$+201=214.8米,
答:A、B两点的距离214.8米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
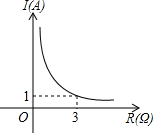 某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )
某闭合电路中,电源的电压为定值,电流I(A)与电阻R(Ω)成反比例.如图所示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I的函数解析式为( )| A. | $I=\frac{2}{R}$ | B. | $I=\frac{3}{R}$ | C. | $I=\frac{5}{R}$ | D. | $I=\frac{6}{R}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=x | B. | y=x-1 | C. | y=x+1 | D. | y=-x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价x元 | … | 70 | 90 | … |
| 销售量y件 | … | 3000 | 1000 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com