
【题目】正方形![]() 中,将一个直角三角板的直角顶点与点
中,将一个直角三角板的直角顶点与点![]() 重合,一条直角边与边
重合,一条直角边与边![]() 交于点
交于点![]() (点
(点![]() 不与点
不与点![]() 和点
和点![]() 重合),另一条直角边与边
重合),另一条直角边与边![]() 的延长线交于点
的延长线交于点![]() .
.
![]() 如图①,求证:
如图①,求证:![]() ;
;
![]() 如图②,此直角三角板有一个角是
如图②,此直角三角板有一个角是![]() ,它的斜边
,它的斜边![]() 与边
与边![]() 交于
交于![]() ,且点
,且点![]() 是斜边
是斜边![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() ;
;
![]() 在
在![]() 的条件下,如果
的条件下,如果![]() ,那么点
,那么点![]() 是否一定是边
是否一定是边![]() 的中点?请说明你的理由.
的中点?请说明你的理由.

【答案】(1)见解析;(2)见解析;(3)点![]() 不一定是边
不一定是边![]() 的中点.
的中点.
【解析】
(1)由正方形的性质可以得出∠B=∠BAD=∠ADC=∠C=90°,AB=AD,由直角三角形的性质∠EAF=∠BAD=90°,就可以得出∠BAE=∠DAF,证明△ABE≌△ADF就可以得出结论;
(2)如图2,连结AG,由且点G是斜边MN的中点,△AMN是等腰直角三角形,就可以得出∠EAG=∠NAG=45°,由△ABE≌△ADF可以得出∠BAE=∠DAF,AE=AF就可以得出△AGE≌AGF,从而得出结论;
(3)设AB=6k,GF=5k,BE=x,就可以得出CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,就有CG=CF﹣GF=k+x,由勾股定理就可以求出x的值而得出结论.
(1)如图①.
∵四边形ABCD是正方形,∴∠B=∠BAD=∠ADC=∠C=90°,AB=AD.
∵∠EAF=90°,∴∠EAF=∠BAD,∴∠EAF﹣∠EAD=∠BAD﹣∠EAD,∴∠BAE=∠DAF.
在△ABE和△ADF中,∵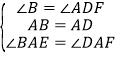 ,∴△ABE≌△ADF(ASA),∴AE=AF;
,∴△ABE≌△ADF(ASA),∴AE=AF;
(2)如图②,连接AG.
∵∠MAN=90°,∠M=45°,∴∠N=∠M=45°,∴AM=AN.
∵点G是斜边MN的中点,∴∠EAG=∠NAG=45°.
在△AGE和AGF中,∵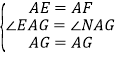 ,∴△AGE≌AGF(SAS),∴EG=GF.
,∴△AGE≌AGF(SAS),∴EG=GF.
∵△ABE≌△ADF,∴BE=DF.
∵GF=GD+DF,∴GF= BE+DG,∴EG=BE+DG;
(3)G不一定是边CD的中点.理由如下:
设AB=6k,GF=5k,BE=x,∴CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,∴CG=CF﹣GF=k+x.在Rt△ECG中,由勾股定理,得:(6k﹣x)2+(k+x)2=(5k)2,解得:x1=2k,x2=3k,∴CG=4k或3k,∴点G不一定是边CD的中点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】一对姐弟中只能有一人参加夏季夏令营,姐弟俩提议让父亲决定.父亲说:现有4张卡片上分别写有1,2,3,4四个整数,先让姐姐随机地抽取一张后放回,再由弟弟随机地抽取一张.若抽取的两张卡片上的数字之和是5的倍数则姐姐参加,若抽取的两张卡片上的数字之和是3的倍数则弟弟参加.试用列表法或树状图分析这种方法对姐弟俩是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 过点(-2,5),和直线
过点(-2,5),和直线![]() ,分别在下列条件下求这个一次函数的解析式.
,分别在下列条件下求这个一次函数的解析式.
(1)它的图象与直线![]() 平行;
平行;
(2)它的图象与y轴的交点和直线![]() 与y轴的交点关于
与y轴的交点关于![]() 轴对称.
轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
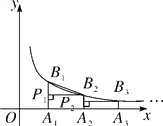
【题目】如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…An-1An=1,分别过点A1,A2,A3,…,An作![]() 轴的垂线交反比例函数
轴的垂线交反比例函数![]() 的图象于点B1,B2,B3,…,Bn,过点B2作
的图象于点B1,B2,B3,…,Bn,过点B2作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ……过点
……过点![]() 作
作![]() 于点
于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,……,
,……,![]() 的面积为
的面积为![]() .求:
.求:
(1)![]() =_____ ___;
=_____ ___;
(2)![]() =___ _____;
=___ _____;
(3)![]() 的和.
的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AEC和△DFB中,∠E=∠F,点A,B,C,D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.

(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果,,那么”);
(2)选择(1)中你写出的一个命题,说明它正确的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E,F,与双曲线y=﹣![]() (x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.
(x<0)交于点P(﹣1,n),且F是PE的中点,直线x=a与l交于点A,与双曲线交于点B(不同于A),PA=PB,则a=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 和直线
和直线![]()
![]() 不论
不论![]() 为何值,直线
为何值,直线![]() 恒交于一定点
恒交于一定点![]() ,求
,求![]() 点坐标;
点坐标;
![]() 当
当![]() 时,设直线
时,设直线![]() 与
与![]() 轴围成的三角形的面积分别为
轴围成的三角形的面积分别为![]() , 求
, 求![]() .
.
![]() 设直线
设直线![]() 交
交![]() 轴为
轴为![]() 点,交
点,交![]() 轴为
轴为![]() 点,原点为
点,原点为![]() 的面积为
的面积为![]() .
.
求①当![]() 时直线
时直线![]() 的条数各是多少;
的条数各是多少;
②当![]() 且
且![]() 时
时![]() 的函数解析式.
的函数解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com