
分析 根据箱中球的个数和不是白球的概率是$\frac{1}{2}$,得出$\frac{1+m}{1+m+n}$=$\frac{1}{2}$,再根据不是黄球的概率是$\frac{2}{3}$,得出$\frac{1+n}{1+m+n}$=$\frac{2}{3}$,求出m、n的值,再代入要求的式子进行计算即可.
解答 解:∵箱子中有1个红球,m个黄球,n个白球,从箱子中随机摸出一个球不是白球的概率是$\frac{1}{2}$,不是黄球的概率是$\frac{2}{3}$,
∴$\frac{1+m}{1+m+n}$=$\frac{1}{2}$,$\frac{1+n}{1+m+n}$=$\frac{2}{3}$,
解得:m=2,n=3,
则mn=23=8.
故答案为:8.
点评 此题考查了概率公式,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
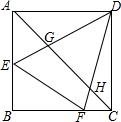 如图,四边形ABCD是正方形,点E、F分别在AB、BC上,∠EDF=45°,DE、DF分别交AC于点G、H.求证:EF=$\sqrt{2}$GH.
如图,四边形ABCD是正方形,点E、F分别在AB、BC上,∠EDF=45°,DE、DF分别交AC于点G、H.求证:EF=$\sqrt{2}$GH.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
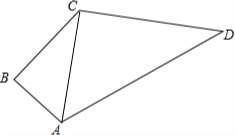 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为4$\sqrt{2}$cm2.
如图,在△ABC中,∠BAC=45°,AB=4cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为4$\sqrt{2}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com