
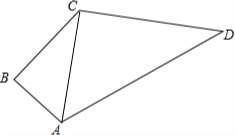
 如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,
如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°,分析 (1)根据勾股定理求出AC,求出AC2+CD2=AD2,根据勾股定理的逆定理求出即可;
(2)分别求出△ABC和△ACD的面积,再相加即可.
解答 解:(1)△ACD是直角三角形,
理由是:由题意可知:在Rt△ABC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵AC2+CD2=52+122=169,AD2=132=169,
∴AC2+CD2=AD2,
∴∠ACD=90°,
即△ACD是直角三角形;
(2)S四边形ABCD=S△ABC+S△ACD
=$\frac{1}{2}$×AB×BC+$\frac{1}{2}$×AC×DC
=$\frac{1}{2}$×3×4+$\frac{1}{2}×$5×12
=36,
即四边形ABCD的面积是36.
点评 本题考查了勾股定理的逆定理,勾股定理的应用,能求出△ACD是直角三角形是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
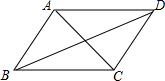 如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )
如图,在四边形ABCD中,给出下列的条件,能判断它是平行四边形的是( )| A. | AB∥CD,AD=BC | B. | ∠B=∠C,∠A=∠D | C. | AB=AD,CB=CD | D. | AB=CD,AD=BC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com