
【题目】某同学在研究二次函数及其图像性质的问题时,发现了两个重要结论:
①抛物线 y = ax 2 2x + 3(a ≠0) ,不论 a 为何值时,它的顶点都在某条直线上;
②抛物线 y = ax 2 2x + 3(a ≠0),其顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到A点,若把顶点的横坐标增加
得到A点,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
(1)请你帮忙求出抛物线 y = ax 2 2x + 3的顶点所在直线的解析式,并证明结论②是正确的;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗,并说明理由;
(3)你能把结论①或②(选择其中之一)推广到一般情况吗,请用数学语言表述你的成 果,并给予严格的证明.
【答案】(1)![]() ,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数
,证明见解析;(2)(0,3),理由见解析;(3)①的推广:若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上;②的推广:抛物线
上;②的推广:抛物线![]()
![]() ,将其顶点的横坐标增加或减少
,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上;证明见解析.
,所得到的两个点一定仍在抛物线上;证明见解析.
【解析】
(1)首先将抛物线y=ax2+2x+3转化成顶点式,写出用a表示的顶点坐标,消去a写出y关于x的表达式;
(2)观察(1)中的顶点坐标![]() ,因为
,因为![]() ,即横坐标
,即横坐标![]() ,纵坐标
,纵坐标![]() ,即可求得结果;
,即可求得结果;
(3)首先写出抛物线的一般形式,再转化成顶点式,将顶点的横坐标增加
代入一般式,验证纵坐标也增加.
解:(1)方法一:
当![]() 时,
时,![]() 的顶点坐标为(1,2),
的顶点坐标为(1,2),
当![]() 时,
时,![]() 的顶点坐标为(1,4),
的顶点坐标为(1,4),
设抛物线![]() 的顶点在直线
的顶点在直线![]() 上,
上,
将(1,2),(1,4)代入,得:
![]() ,解得:
,解得:![]() ,
,
所以![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
方法二:
易知![]() 的顶点是
的顶点是![]() ,
,
即![]() ,
,![]() ,
,
消去a得:![]() ,
,
即抛物线![]() 的顶点在直线
的顶点在直线![]() ;
;
证明:抛物线![]() 的顶点是
的顶点是![]() ,
,
由题意得:A(0,3),B(![]() ,3),
,3),
当x=0时,y=3,则点A在抛物线![]() 上,
上,
当x=![]() 时,
时,![]() ,则点B抛物线
,则点B抛物线![]() 上,
上,
(2)直线![]() 上有一点(0,3)不是该抛物线的顶点,
上有一点(0,3)不是该抛物线的顶点,
抛物线![]() 的顶点是
的顶点是![]() ,
,
当![]() 时,横坐标
时,横坐标![]() ,即(0,3)不是抛物线的顶点;
,即(0,3)不是抛物线的顶点;
(3)①的推广
若b、c是常数,对任意的实数![]() ,抛物线
,抛物线![]() 的顶点在直线
的顶点在直线![]() 上.
上.
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
当![]() 时,则
时,则![]() 的顶点为
的顶点为![]() ,
,
将它们代入![]() 得:
得:
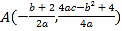 ,
,
解得:![]()
则直线为![]() ,
,
事实上,![]() 时,
时,
![]() ,
,
即抛物线顶点![]() 在直线
在直线![]() 上;
上;
②的推广
猜想:抛物线y = ax 2 2x + 3(a ≠0) ,将其顶点的横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,所得到的两个点一定仍在抛物线上.
,所得到的两个点一定仍在抛物线上.
证明:抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,
,
将其横坐标增加或减少![]() ,纵坐标增加
,纵坐标增加![]() ,得到
,得到
![]() ,
,![]()
将![]() 代入
代入![]() 得
得
![]()
=![]()
=![]()
∴点A在抛物线![]() 上,同理可证点B也在抛物线上.
上,同理可证点B也在抛物线上.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为A,B(点A 在点B的左侧).
轴的交点为A,B(点A 在点B的左侧).
(1)求点A,B的坐标;
(2)横、纵坐标都是整数的点叫整点.
①直接写出线段AB上整点的个数;
②将抛物线![]() 沿
沿![]() 翻折,得到新抛物线,直接写出新抛物线在
翻折,得到新抛物线,直接写出新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)整点的个数.
所围成的区域内(包括边界)整点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
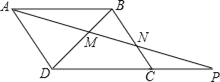
【题目】如图,已知四边形ABCD是平行四边形,P为DC延长线上一点,AP分别交BD,BC于点M,N.
(1)图中相似三角形共有_____对;
(2)证明:AM2=MNMP;
(3)若AD=6,DC:CP=2:1,求BN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点(3,﹣3).
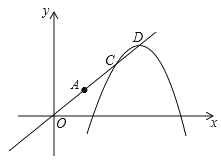
(1)求抛物线的解析式及顶点A的坐标;
(2)将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,如图,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(中考·安徽)如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
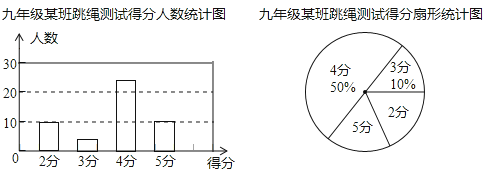
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点C是∠AOB的平分线上一点,点P、P′分别在边OA、OB上.如果要得到 OP=OP′,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为( )
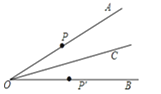
①∠OCP=∠OCP′;②∠OPC=∠OP′C;③PC=P′C;④PP′⊥OC.
A.①②B.④③C.①④③D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com