
【题目】解方程
(1)![]() (直接开方法)
(直接开方法)
(2)![]() (配方法)
(配方法)
(3)![]() (公式法)
(公式法)
(4)![]() (因式分解法)
(因式分解法)
(5)![]()
(6)![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() ,
,![]() ;(5)
;(5)![]() ,
,![]() ;(6)
;(6)![]() .
.
【解析】
(1)根据直接开方法的步骤进行求解;
(2)根据配方法的步骤进行求解;
(3)根据公式法的步骤进行求解;
(4)根据因式分解法的步骤进行求解;
(5)根据因式分解法的步骤进行求解;
(6)将分式方程化成整式方程,求出整式方程的解,再进行检验即可.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(2)移项得:![]() ,
,
配方得:![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(3)方程整理得:![]() ,
,
∵a=3,b=-2,c=-6,
∴△=4+72=76>0,
∴![]() ,
,
∴![]() ,
,![]() ;
;
(4)移项得:![]() ,
,
因式分解得:![]() ,
,
∴x-2=0或3x+2=0,
∴![]() ,
,![]() ;
;
(5)因式分解得:![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() ,
,![]() ;
;
(6)方程两边同乘![]() 得:
得:![]() ,
,
解得:![]() ,
,
检验:当![]() 时,
时,![]() ,
,
故原方程的解为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,且
,且![]() 。
。
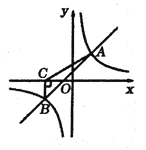
(1)求一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式![]() 的解集;
的解集;
(3)若![]() 是反比例函数
是反比例函数![]() 图象上的两点,且
图象上的两点,且![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,
,![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中一定正确的是( ).
,其中一定正确的是( ).
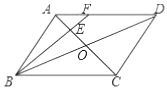
A.①②③④B.①②C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一种产品2017年的产量是100万件,计划2019年产量达到121万件.假设2017年到2019年这种产品产量的年增长率相同.
(1)求2017年到2019年这种产品产量的年增长率;
(2)2018年这种产品的产量应达到多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,张老师出示了一个题目:“如图,ABCD的对角线相交于点O,过点O作EF垂直于BD交AB,CD分别于点F,E,连接DF,![]() 请根据上述条件,写出一个正确结论
请根据上述条件,写出一个正确结论![]() ”其中四位同学写出的结论如下:
”其中四位同学写出的结论如下:
小青:![]() ;小何:四边形DFBE是正方形;
;小何:四边形DFBE是正方形;
小夏:![]() ;小雨:
;小雨:![]() .
.
这四位同学写出的结论中不正确的是![]()
![]()

A. 小青 B. 小何 C. 小夏 D. 小雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在研究二次函数及其图像性质的问题时,发现了两个重要结论:
①抛物线 y = ax 2 2x + 3(a ≠0) ,不论 a 为何值时,它的顶点都在某条直线上;
②抛物线 y = ax 2 2x + 3(a ≠0),其顶点的横坐标减少![]() ,纵坐标增加
,纵坐标增加![]() 得到A点,若把顶点的横坐标增加
得到A点,若把顶点的横坐标增加![]() ,纵坐标增加
,纵坐标增加![]() ,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
,得到B点,则A,B两点一定在抛物线y = ax 2 2x + 3上.
(1)请你帮忙求出抛物线 y = ax 2 2x + 3的顶点所在直线的解析式,并证明结论②是正确的;
(2)问题(1)中的直线上有一个点不是该抛物线的顶点,你能找出它来吗,并说明理由;
(3)你能把结论①或②(选择其中之一)推广到一般情况吗,请用数学语言表述你的成 果,并给予严格的证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒
与x轴、y轴分别交于A、B两点,点P从点A出发,沿折线AB﹣BO向终点O运动,在AB上以每秒5个单位长度的速度运动,在BO上以每秒3个单位长度的速度运动;点Q从点O出发,沿OA方向以每秒![]() 个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
个单位长度的速度运动.P,Q两点同时出发,当点P停止时,点Q也随之停止.过点P作PE⊥AO于点E,以PE,EQ为邻边作矩形PEQF,设矩形PEQF与△ABO重叠部分图形的面积为S,点P运动的时间为t秒.
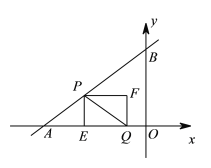
(1)连结PQ,当PQ与△ABO的一边平行时,求t的值;
(2)求S与t之间的函数关系式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AD=BD,将△ABD绕点A逆时针旋转得到△ACE,使点C落在直线BD上.
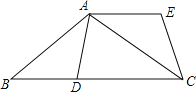
(1)求证:AE∥BC;
(2)连接DE,判断四边形ABDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com