
【题目】如图,已知正方形ABCD的边长为2,以点A为圆心,1为半径作圆,E是A上的任意一点,将点E绕点D按逆时针方向旋转90°,得到点F,连接AF,则AF的最大值是_____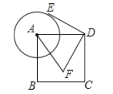
【答案】![]() +1
+1
【解析】
先找出AF最大值时,点E的位置,再判断出AF最大时,点C在AF上,根据正方形的性质求出AC,从而得出AF的最大值
过点A作∠EAB=45°交A于点E,此时旋转后AF最大,过点E作EG⊥AD交DA延长线于G,
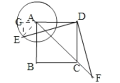
在Rt△AEG中,AE=1,∠GAE=∠EAB=45°
∴EG=AG=![]() ,
,
∵∠ADC=∠EDF
∴∠ADE=∠CDF
∵在△ADE和△CDF中,
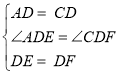
∴△ADE△CDF
∴CF=AE=1
∵∠DCF=∠DAE=∠BAD+∠EAB=90°+45°=135°
∴点C在线段AF上,
∴AF=AC+ CF
∵AC是边长为2的正方形的对角线,
∴AC=![]()
∴AF=![]() +1
+1
即:AF的最大值是![]() +1,
+1,
故答案为:![]() +1.
+1.


 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3过A(﹣3,0),B(1,0)两点,交y轴于点C.
(1)求该抛物线的表达式.
(2)设P是该抛物线上的动点,当△PAB的面积等于△ABC的面积时,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近端午节,某食品店每天卖出300只粽子,卖出一只粽子的利润为1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获得的利润更多,该店决定把零售单价下降m(0<m<1)元,
(1)零售单价降价后,每只利润为 元,该店每天可售出 只粽子.
(2)在不考虑其他因素的条件下,当零售单价下降多少元时,才能使该店每天获取的利润是420元,且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
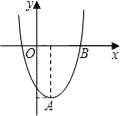
【题目】在直角坐标平面内,二次函数图象的顶点为A(1,﹣4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作体验)
如图①,已知线段AB和直线l,用直尺和圆规在l上作出所有的点P,使得∠APB=30°,如图②,小明的作图方法如下: 
第一步:分别以点A,B为圆心,AB长为半径作弧,两弧在AB上方交于点O;
第二步:连接OA,OB;
第三步:以O为圆心,OA长为半径作⊙O,交l于![]() ;
;
所以图中![]() 即为所求的点.(1)在图②中,连接
即为所求的点.(1)在图②中,连接![]() ,说明∠
,说明∠![]() =30°
=30°
(方法迁移)
(2)如图③,用直尺和圆规在矩形ABCD内作出所有的点P,使得∠BPC=45°,(不写做法,保留作图痕迹).
(深入探究)
(3)已知矩形ABCD,BC=2.AB=m,P为AD边上的点,若满足∠BPC=45°的点P恰有两个,则m的取值范围为________.
(4)已知矩形ABCD,AB=3,BC=2,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,E是BC边上的一点,将矩形ABCD沿折痕AE折叠,使得顶点B落在CD边上的点P处,PC=4(如图1).
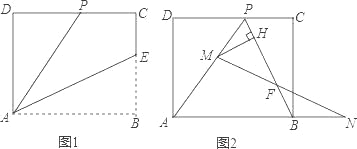
(1)求AB的长;
(2)擦去折痕AE,连结PB,设M是线段PA的一个动点(点M与点P、A不重合).N是AB沿长线上的一个动点,并且满足PM=BN.过点M作MH⊥PB,垂足为H,连结MN交PB于点F(如图2).
①若M是PA的中点,求MH的长;
②试问当点M、N在移动过程中,线段FH的长度是否发生变化?若变化,说明理由;若不变,求出线段FH的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且
,点M是AB的中点,连接MC,点P是线段BC延长线上一点,且![]() ,连接MP交AC于点H.将射线MP绕点M逆时针旋转
,连接MP交AC于点H.将射线MP绕点M逆时针旋转![]() 交线段CA的延长线于点D.
交线段CA的延长线于点D.
(1)找出与![]() 相等的角,并说明理由.
相等的角,并说明理由.
(2)如图2,![]() ,求
,求![]() 的值.
的值.
(3)在(2)的条件下,若![]() ,求线段AB的长.
,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形。

(1)求证AE=CG,并说明理由。
(2)连接AG,若AB=17,DG=13,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com