练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
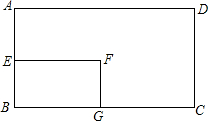
    8．如图，矩形ABCD的面积是72，AE=$\frac{1}{2}$DC，EF=$\frac{1}{2}$AD，那么矩形EBGF的面积是（　　）
    A．24B．18C．12D．9

    分析 先根据题意判断出矩形ABCD∽矩形EBGF，再由相似多边形的性质即可得出结论．

    解答 解：∵AE=$\frac{1}{2}$DC，EF=$\frac{1}{2}$AD，
    ∴矩形ABCD∽矩形EBGF，相似比为2：1．
    ∵矩形ABCD的面积是72，
    ∴$\frac{{S}_{矩形ABCD}}{{S}_{矩形EBGF}}$=$\frac{72}{{S}_{矩形EBGF}}$=（$\frac{2}{1}$）2，解得S矩形EBGF=$\frac{72}{4}$=18．
    故选B．

    点评 本题考查的是相似多边形的性质，熟知相似多边形对应边的比叫做相似比，面积的比等于相似比的平方是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

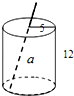    18．如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（　　）
    A．5≤a≤12B．5≤a≤13C．12≤a≤13D．12≤a≤15

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．在△ABC中，∠C=90°，a=5，c=13，用计算器求∠A约等于（　　）
    A．14°38′B．65°22′C．67°23′D．22°37′

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．在Rt△ABC中，如果各边的长度都扩大2倍，那么锐角A的正弦值与余弦值（　　）
    A．都不变B．都扩大2倍C．都缩小$\frac{1}{2}$D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在△ABC中，∠C=90°，AC=3BC，则sinA=$\frac{\sqrt{10}}{10}$，cosA=$\frac{3\sqrt{10}}{10}$，tanA=$\frac{1}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．一列快车长306m，一列慢车长344m，两车相向而行，从相遇到离开需要13s，如果同向而行，快车从追及到超过慢车需要65s，求快车、慢车各自的速度．若设快车速度为x m/s，慢车速度为y m/s，那么，由题意列出的方程为（　　）
    A．$\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344\end{array}$B．$\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344+306\end{array}$
    C．$\left\{\begin{array}{l}13（x+y）=306+344\\ 65（x-y）=344-306\end{array}$D．$\left\{\begin{array}{l}344y=306x\\ 65（x-y）=344+306\end{array}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知正比例函数y=（m+1）x+m2-4，若y随x的增大而减小，则m的值是-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知△ABC与△A′B′C′的相似比为1：2，△ABC的周长为30cm，并且△A′B′C′的三边比为4：5：6，则△A′B′C′的最长边为（　　）
    A．44cmB．40cmC．36cmD．24cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在0.458，4.$\stackrel{•}{2}$，$\frac{π}{2}$，$\sqrt{0.4}$，-$\root{3}{0.001}$，$\frac{1}{7}$这几个数中无理数有2个．

    查看答案和解析>>

    同步练习册答案