【题目】在正方形ABCD中，

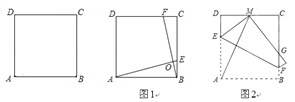
（1）如图1，若点E，F分别在边BC，CD上，AE，BF交于点O，且∠AOF=90°.求证：AE =BF．

（2）如图2，将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．若DC=5,CM=2，求EF的长．

参考答案：

【答案】(1)证明见解析;(2) .

【解析】(1) 分析：（1）根据矩形的对边平行且相等得到AB=BC，∠DCB=∠ABE．再结合一对直角相等即可证明三角形全等；(2) 由折叠的性质得全等三角形的对应边相等以及勾股定理，可以求得DF，EF的长；再根据勾股定理求得DE的长，运用三角函数定义求解．

本题解析：

(1)证明：∵四边形ABCD是正方形，∴AB=BC，

∠ABE=∠BCF=90°，∵∠AOF=90°，∠AOB=90°，

∴∠BAE+∠OBA=90°，又∵∠FBC+∠OBA=90°，

∴∠BAE=∠CBF（同角的余角相等），在△ABE和△BCF中

∴

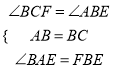
∴△ABE≌△BCF（ASA）．∴AE=BF．

(2) 作MG⊥AB于G，作FH⊥AD于H，如图所示：

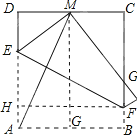
则MG=AD，FH=AB，∴MG=FH，

在△AMG和△EFH中, ，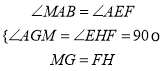

∴△AMG≌△EFH(AAS)，∴AM=EF；∵DC=AD=5,CM=2,∴DM=5-2=3

在Rt△ADM中,根据勾股定理得：AM=，

∴EF=AM=.

关闭