
为了提高学生书写汉字的能力,某市举办了“汉字听写大赛”.为了决定谁将获得仅有的一张观赛券,小王和小李设计了如下的一个规则:不透明的甲袋中有编号分别为1,2,3的乒乓球三个,不透明的乙袋中有编号分别为4,5的乒乓球两个,五个球除了编号不同外,其他均相同.小王和小李分别从甲、乙两个袋子中随机地各摸出一个球,若所摸出的两个球上的数字之和为奇数,则小王去;若两个球上的数字之和为偶数,则小李去.试用列表法或画树状图的方法分析这个规则对双方是否公平?
【考点】游戏公平性;列表法与树状图法.
【分析】依据题意先用列表法或画树状图法分析所有等可能的结果,然后根据概率公式求出小王和小李摸球的概率即可得到规则对双方是否公平.
【解答】解:列表得:
| 甲袋 和 乙袋 | 2 | 3 | 1 |
| 5 | 7 | 8 | 6 |
| 4 | 6 | 7 | 5 |
由列表可知所有可能的结果有6种,和为奇数有3种,和偶数有三种, 所以P(两个球上的数字之和为奇数)=
所以P(两个球上的数字之和为奇数)=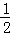 ,P(两个球上的数字之和为偶数)=
,P(两个球上的数字之和为偶数)=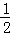 ,
,
所以这个规则公平.
【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
如图1,平面直角坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线y1=ax(x﹣t)(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
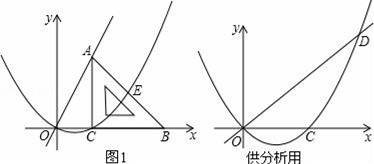

(1)填空:用含t的代数式表示点A的坐标及k的值:A ,k= ;
(2)随着三角板的滑动,当a=
 时:
时:
①请你验证:抛物线y1=ax(x﹣t)的顶点在函数y=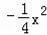
 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
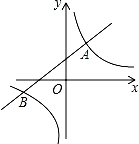
如图,双曲线y=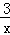 与直线y=
与直线y= x+1交于A、B两点,A点在B点的右侧.
x+1交于A、B两点,A点在B点的右侧.
(1)求A、B点的坐标;
(2)点C是双曲线上一点,点D是x轴上一点,是否存在点D,使以A、B、C、D为顶点的四边形是平行四边形?如果存在,写出求解过程和点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=﹣2x2+1向右平移1个单位,再向下平移3个单位后所得到的抛物线为( )
A.y=﹣2(x+1)2﹣2 B.y=﹣2(x+1)2﹣4 C.y=﹣2(x﹣1)2﹣2 D.y=﹣2(x﹣1)2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
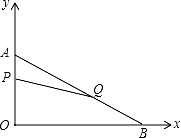
在平面直角坐标系内,已知点A(0,6),点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
(1)求直线AB的解析式;
(2)当t=2秒时,求四边形OPQB的面积;
(3)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com