
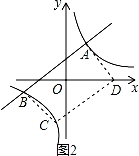
如图,双曲线y=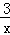 与直线y=
与直线y= x+1交于A、B两点,A点在B点的右侧.
x+1交于A、B两点,A点在B点的右侧.
(1)求A、B点的坐标;
(2)点C是双曲线上一点,点D是x轴上一点,是否存在点D,使以A、B、C、D为顶点的四边形是平行四边形?如果存在,写出求解过程和点D的坐标;若不存在,请说明理由.
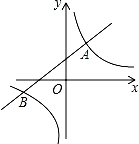
【考点】反比例函数综合题.
【分析】(1)联立一次函数与反比例函数的解析式即可得出A、B两点的坐标;
(2)根据AB两点的坐标可求出线段AB的水平距离与竖直距离,再根据AB为平行四边形的边与对角线两种情况进行讨论即可.
【解答】解:(1)由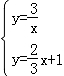 消去y得,2x2+3x﹣9=0,
消去y得,2x2+3x﹣9=0,
解得x1=﹣3,x2=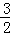 ,
,
点A的坐标为(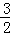 ,2),点B的坐标为(﹣3,﹣1).
,2),点B的坐标为(﹣3,﹣1).
(2)∵A(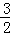 ,2),B(﹣3,﹣1),
,2),B(﹣3,﹣1),
∴线段AB的垂直距离为2﹣(﹣1)=3,水平距离为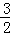 ﹣(﹣3)=
﹣(﹣3)=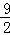 .
.
①令y=3,由y=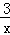 得x=1,则1﹣
得x=1,则1﹣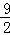 =﹣
=﹣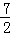 ,
,
∴点D的坐标(﹣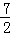 ,0);
,0);
②令y=﹣3,由y=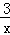 得x=﹣1,则﹣1+
得x=﹣1,则﹣1+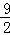 =
=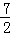 ,
,
∴点D的坐标(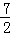 ,0);
,0);
③如图,线段AB的中点E的坐标为(﹣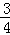 ,
,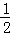 ),过点C作CF⊥x轴于点G,点E作EG⊥OF于x轴点G,
),过点C作CF⊥x轴于点G,点E作EG⊥OF于x轴点G,
则EG=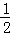 ,
,
∵EG是△CDF的中位线
∴CF=2EG=1,即F点的纵坐标为1,
∴C(3,1),
∴F(3,0).
∴DG=GF,即3+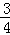 =﹣
=﹣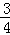 ﹣x,解得x=﹣
﹣x,解得x=﹣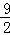 .
.
点D的坐标(﹣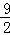 ,0).
,0).
综上所述,D点坐标为(﹣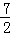 ,0),(
,0),(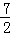 ,0)或(﹣
,0)或(﹣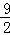 ,0
,0 ).
).


【点评】本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、平行四边形的判定与性质等知识,在解答(2)时要注意进行分类讨论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
“服务他人,提升自我”,七一学校积极开展志愿者服务活动,来自初三的5名同学(3男两女)成立了“交通秩序维护”小分队,若从该小分队中任选两名同学进行交通秩序维护,则恰好是一男一女的概率是( )
A.
 B.
B.
 C.
C.
 D.
D.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
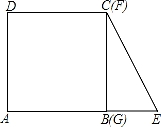
A.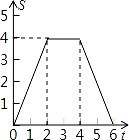 B.
B.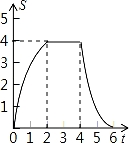 C.
C.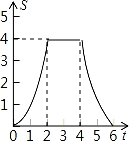 D.
D.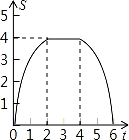
查看答案和解析>>
科目:初中数学 来源: 题型:
为了提高学生书写汉字的能力,某市举办了“汉字听写大赛”.为了决定谁将获得仅有的一张观赛券,小王和小李设计了如下的一个规则:不透明的甲袋中有编号分别为1,2,3的乒乓球三个,不透明的乙袋中有编号分别为4,5的乒乓球两个,五个球除了编号不同外,其他均相同.小王和小李分别从甲、乙两个袋子中随机地各摸出一个球,若所摸出的两个球上的数字之和为奇数,则小王去;若两个球上的数字之和为偶数,则小李去.试用列表法或画树状图的方法分析这个规则对双方是否公平?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
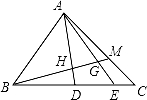
A.3:2:1 B.5:3:1 C.25:12:5 D.51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:一次函数y=kx+b中,当自变量x=3时,函数值y=5;当x=﹣4时,y=﹣9.
(1)求这个一次函数解析式;
(2)解关于x的不等式kx+b≤7的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com