Question

8．如图，在△ABC中，以AB为直径的⊙O，交BC于点D，且BD=CD，交直线AC于点E，连接BE．
（1）如图1，求证：∠CAB=2∠CBE；
（2）如图2，过D作DF⊥AB于F，求证：BE=2DF；
（3）如图3，在（2）的条件下，在∠BDF的内部作∠BDM，使∠BDM=∠ABE，DM分别交AB、BE于点N、G，交⊙O于点M，若DF=$\sqrt{2}$BN=2$\sqrt{3}$，求MG的长．

Answer 1

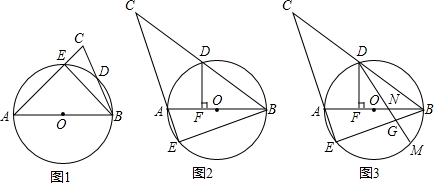
分析 （1）连接AD，由AB为⊙O的直径，得到∠ADB=90°，推出AD垂直平分BC，AB=AC，得到AD平分∠BAC，即可得到结论；
（2）延长DF交⊙O于K，连接DE，由AB为⊙O的直径，得到∠AEB=90°，于是得到DE=$\frac{1}{2}$BC，推出DF=FK，BK=BD，求得DK=2DF，BK=DE，等量代换即可得到结论；
（3）连接AD，连接ED，由BE=2DF，DF=2$\sqrt{3}$，得到BE=4$\sqrt{3}$，求得BN=$\sqrt{6}$，推出△DAE≌△DNB，根据全等三角形的性质得到AE=NB=$\sqrt{6}$，解直角三角形求得CE=AC+AE=4$\sqrt{6}$，过G作GH⊥BD于H，则在Rt△GHD中，tan∠GDH=$\frac{GH}{DH}$=$\frac{\sqrt{2}}{4}$，设GH=$\sqrt{2}$a，DH=4a，于是得到tan∠GBH=$\frac{GH}{BH}$=$\frac{\sqrt{2}a}{BH}$=$\sqrt{2}$，推出DH=$\frac{24}{5}$，GH=$\frac{6}{5}$$\sqrt{2}$，由勾股定理得到D=$\frac{18}{5}$$\sqrt{2}$，连接BM，推出△GDB∽△BDM，根据相似三角形的性质得到$\frac{BD}{DM}=\frac{DG}{DB}$，代入数据即可得到结论．

解答 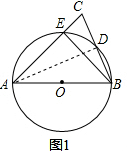（1）证明：连接AD
∵AB为⊙O的直径，
∴∠ADB=90°，
∴AD⊥BC，
又∵BD=CD，
∴AD垂直平分BC，AB=AC，
∴AD平分∠BAC，
∴∠CAB=2∠CAD，
∵∠CAD=∠CBE，
∴∠CAB=2∠CBE，

（2）证明：延长DF交⊙O于K，连接DE，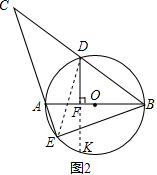
∵AB为⊙O的直径，
∴∠AEB=90°，
∵BD=CD，
∴DE=$\frac{1}{2}$BC，
∴DE=BD=CD，
∴DE=DB，
∵AB⊥DK，且AB为⊙O的直径，
∴DF=FK，BK=BD，
∴DK=2DF，BK=DE，
∴BK+EK=DE+EK，
∴DK=BE，
∴DK=BE，
∴BE=2DF，

（3）解：连接AD，连接ED，
∵BE=2DF，DF=2$\sqrt{3}$，
∴BE=4$\sqrt{3}$，
∵$\sqrt{2}$BN=2$\sqrt{3}$，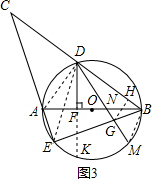
∴BN=$\sqrt{6}$，
∵∠BDM=∠ABE∠ADE=∠ABE，
∴∠ADE=∠BDM，
在△DAE与△DNB中，$\left\{\begin{array}{l}{∠ADE=∠BDM}\\{DE=DB}\\{∠AED=∠DBN}\end{array}\right.$，
∴△DAE≌△DNB，
∴AE=NB=$\sqrt{6}$，
在Rt△AEB中，AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=3$\sqrt{6}$，
tan∠ABE=$\frac{AE}{BE}=\frac{\sqrt{6}}{4\sqrt{3}}$=$\frac{\sqrt{2}}{4}$，
∴AC=AB=3$\sqrt{6}$，tan∠BDG=$\frac{\sqrt{2}}{4}$，
∴CE=AC+AE=4$\sqrt{6}$，
在Rt△CEB中，tan∠CBE=$\frac{CE}{BE}=\frac{4\sqrt{6}}{4\sqrt{3}}$=$\sqrt{2}$，
过G作GH⊥BD于H，则在Rt△GHD中，tan∠GDH=$\frac{GH}{DH}$=$\frac{\sqrt{2}}{4}$，
设GH=$\sqrt{2}$a，DH=4a，
∴在Rt△GHB中，tan∠GBH=$\frac{GH}{BH}$=$\frac{\sqrt{2}a}{BH}$=$\sqrt{2}$，
∴BH=a，
∴BD=BH+DH=a+4a=6，
∴a=$\frac{6}{5}$，
∴DH=$\frac{24}{5}$，GH=$\frac{6}{5}$$\sqrt{2}$，
在Rt△DHG中，DG=$\sqrt{D{H}^{2}+G{H}^{2}}$=$\sqrt{（\frac{24}{5}）^{2}+（\frac{6\sqrt{2}}{5}）^{2}}$=$\frac{18}{5}$$\sqrt{2}$，
连接BM，
∵DB=DE，
∴∠DEB=∠DBE，
∵∠DEB=∠M，
∴∠DBG=∠M，
∵∠GDB=∠BDM，
∴△GDB∽△BDM，
∴$\frac{BD}{DM}=\frac{DG}{DB}$，即$\frac{6}{DM}=\frac{\frac{18}{5}\sqrt{2}}{6}$，
∴DM=5$\sqrt{2}$，
∴MG=DM-DG=$\frac{7}{5}$$\sqrt{2}$．

点评 本题考查了全等三角形的判定和性质，相似三角形的判定和性质，线段的垂直平分线的性质，圆周角定理，锐角三角函数，正确的作出辅助线是解题的关键．