
����Ŀ���ۺ���ʵ����
���ֲ�������ͼ1���ı���![]() ��һ�ž���ֽƬ��
��һ�ž���ֽƬ��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϣ���
���ϣ���![]() ������
������![]() ��
��![]() .��
.��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �۵�����
�۵�����![]() ��
��![]() �ֱ����ڵ�
�ֱ����ڵ�![]() ��
��![]() ��.
��.
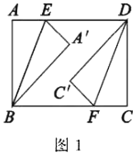
̽��չʾ��
��1�����̿�С�顱���֣�![]() ����
����![]() ����չʾ�����µ�֤������.
����չʾ�����µ�֤������.
֤�����ھ���![]() �У�
��![]() ��
��![]() ��
��![]() .
.
�֡�![]() ��
��
��![]() .
.
��![]() ��
��![]() .
.
��![]() ��
��
��![]() .������1��
.������1��
��![]() .
.
��![]() .������2��
.������2��
��˼������������֤�������еġ�����1���롰����2���ֱ�ָʲô��
�ڡ��ڷ�С�顱��Ϊ��������ͨ��֤���ı���![]() ��ƽ���ı��λ�֤��������ݡ��ڷ�С�顱��֤��˼·д��֤������.
��ƽ���ı��λ�֤��������ݡ��ڷ�С�顱��֤��˼·д��֤������.
����֤����
��2����ͼ2���۵������У�����![]() ��
��![]() ��ֱ��
��ֱ��![]() ��ͬ��ʱ���ӳ�
��ͬ��ʱ���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() �����ı���
�����ı���![]() ��ʲô�����ı��Σ���˵������.
��ʲô�����ı��Σ���˵������.
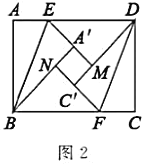
�����ع㣺
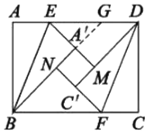
��3����ͼ3������![]() ��
��![]() ��
��![]() .
.

�ٵ�![]() ʱ��
ʱ��![]() �ij�Ϊ________��
�ij�Ϊ________��
��![]() �ij������ֵ�����У�����ֱ��д��
�ij������ֵ�����У�����ֱ��д��![]() �������ֵ�ʹ�ʱ�ı���
�������ֵ�ʹ�ʱ�ı���![]() ����״����û�У���˵������.
����״����û�У���˵������.
���𰸡���1���ټ������ڼ���������2�����Σ����ɼ���������3����![]() ���У�
����![]() ������
������
��������
��1���ٸ���ƽ���ߵ��ж������ʼ��ɵý⣻
���ɾ��ε����ʽ��е���ת���ó�![]() �������ж��ı���
�������ж��ı���![]() ��ƽ���ı��Σ����ɵ�֤��
��ƽ���ı��Σ����ɵ�֤��
��2�������ɶ��۵����ʵó�![]() ��
��![]() ��Ȼ������
��Ȼ������![]() �����е���ת�����ó�
�����е���ת�����ó�![]() �������ж��ı���
�������ж��ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��3�����ӳ�C��A����AD��G��A��C����BC��H�����á�A��GE�ա�C��HF���ó�AG=BH=4�������ù��ɶ����������̣����ɵó�AE��
�ڵ�![]() ��BDʱ��
��BDʱ��![]() �ij������ֵ���������ε������Լ����ɶ������ɵý�.
�ij������ֵ���������ε������Լ����ɶ������ɵý�.
��1���١�����1��ָ��ֱ��ƽ�У��ڴ�����ȣ�
������2��ָͬλ����ȣ���ֱ��ƽ��.
��֤�����ھ���![]() �У�
��![]() ��
��![]() .
.
�֡�![]() ��
��
��![]() ����
����![]() .
.
���ı���![]() ��ƽ���ı���.
��ƽ���ı���.
��![]() ����
����![]() .
.
��2���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
�ӳ�![]() ����
����![]() �ڵ�
�ڵ�![]() ������ͼ.
������ͼ.
�ɶ��ۿ�֪��![]() .
.
��![]() ��
��
��![]() .
.
ͬ����![]() .
.
�ɣ�1���ã�![]() ��
��
��![]() .
.
�ɶ��ۿ�֪��![]() ��
��![]() .
.
��![]()
��![]() ��
�У�![]() .
.
�ھ���![]() �У�
��![]() ����
����![]() .
.
��![]() .
.
��![]() .
.
��![]() .
.
��![]() .
.
���ı���![]() �Ǿ���.
�Ǿ���.
��3�����ӳ�C��A����AD��G��A��C����BC��H����ͼ��ʾ��
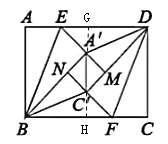
��![]()
��GH��AB
���A��GE=��C��HF=90����AG=BH
�ߡ�EA��G=��FC��H��A��E=C��F
���A��GE�ա�C��HF
��EG=FH
��AE=CF
��AG=CH
��AG=BH=4
��![]()
��![]()
��AE=x����EG=4-x��
��Rt��A��EG��![]()
��![]()
���![]() ����AE=
����AE=![]() ��
��
�ڵ�![]() ��BDʱ��
��BDʱ��![]() �ij������ֵ�����ֵΪ
�ij������ֵ�����ֵΪ![]()
![]() ����ʱ�ı���
����ʱ�ı���![]() ������.
������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ��
��![]() �ĶԱ߷ֱ���
�ĶԱ߷ֱ���![]() ��
��![]() ��
��![]() ��һ��ֱ��
��һ��ֱ��![]() ���
���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() �����
�����![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
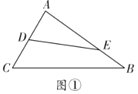
��1����ͼ�٣���![]() ��
��![]() �ֳ��ܳ���ȵ������֣���
�ֳ��ܳ���ȵ������֣���![]() ��ֵ��(��
��ֵ��(��![]() ��
��![]() ��
��![]() ��ʾ)
��ʾ)
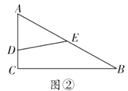
��2����ͼ�ڣ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֳ��ܳ��������ȵ������֣���
�ֳ��ܳ��������ȵ������֣���![]() ��ֵ��
��ֵ��
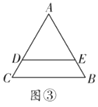
��3����ͼ�ۣ���![]() ��
��![]() �ֳ��ܳ��������ȵ������֣���
�ֳ��ܳ��������ȵ������֣���![]() ����
����![]() ��
��![]() ��
��![]() ����ʲô��ϵ��
����ʲô��ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
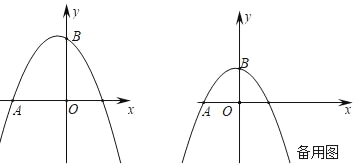
����Ŀ����֪������y��ax2��![]() x+c����A(��2��0)��B(0��2)���㣬����P��Qͬʱ��ԭ���������1����λ/����ٶ��˶�������P��x���������˶�������Q��y���������˶�������PQ�����˶�ʱ��Ϊt��
x+c����A(��2��0)��B(0��2)���㣬����P��Qͬʱ��ԭ���������1����λ/����ٶ��˶�������P��x���������˶�������Q��y���������˶�������PQ�����˶�ʱ��Ϊt��
(1)�������ߵĽ���ʽ��
(2)��BQ��![]() APʱ����t��ֵ��
APʱ����t��ֵ��
(3)���ŵ�P��Q���˶������������Ƿ���ڵ�M��ʹ��MPQΪ�ȱ������Σ������ڣ������t��ֵ����Ӧ��M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪӭ������ѧ������������ƻ�����A��B��������20����ѧ��ѵ��ʹ�ã�������A������6���������������������720Ԫ��������A������12������ʵ�������������840Ԫ��
��1��A��B���������赥�۸�����Ԫ��
��2���蹺��A������x����A����������8�����������ΪyԪ����ȷ��y��x�Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
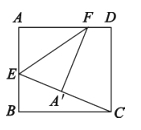
����Ŀ����ͼ���ھ���![]() �У�
�У�![]() �ֱ��DZ�
�ֱ��DZ�![]() �ϵĵ㣬
�ϵĵ㣬![]() ����
����![]() ��
��![]() ����ֱ���۵�����
����ֱ���۵�����![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ���������߶�
���������߶�![]() �ϣ���
�ϣ���![]() �����ۺ�
�����ۺ�![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
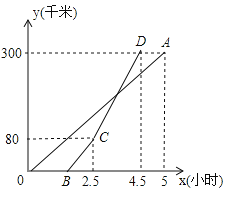
����Ŀ����ͼ���ס����������![]() ��һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵأ��߶�
��һ��������һ���γ��Ⱥ�Ӽس���ʻ���ҵأ��߶�![]() ������
������![]() �ֱ��ʾ�����ͽγ���صľ���
�ֱ��ʾ�����ͽγ���صľ���![]()
![]() ���������ʱ��
���������ʱ��![]()
![]() ֮��ĺ�����ϵ�������ͼ�����������⣺
֮��ĺ�����ϵ�������ͼ�����������⣺
��1���������ٶ�Ϊ___________![]() �����γ������ҵغ�,�������ҵصľ���Ϊ____________ǧ�ף�
�����γ������ҵغ�,�������ҵصľ���Ϊ____________ǧ�ף�
��2����γ��ı��ٶȺ�![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��3���γ������ҵغ�������ԭ·��![]() ���ٶȷ��أ���γ����ҵس�����ʱ���ٴ������������
���ٶȷ��أ���γ����ҵس�����ʱ���ٴ������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�㲶�㴬��A����������źţ�λ��A�����������B����һ�Ҿ�Ԯͧ����ǰȥ��Ԯ��������֮���д�Ƭ��������ֱ�ߵ����Ԯͧ�������ϵ�����������ƫ��![]() ����ÿСʱ30������ٶȺ��У�ͬʱ���㴬���������ٺ��У�30���Ӻ��㴬�������A��
����ÿСʱ30������ٶȺ��У�ͬʱ���㴬���������ٺ��У�30���Ӻ��㴬�������A��![]() �����D������ʱ��Ԯͧ��C�����D������ƫ��
�����D������ʱ��Ԯͧ��C�����D������ƫ��![]() �ķ����ϣ�
�ķ����ϣ�
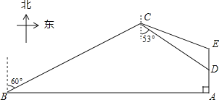
![]() ��C��D����ľ��룻
��C��D����ľ��룻
![]() ���㴬�����������У���Ԯͧ�����ٴε���������CE����ǰȥ��Ԯ�����Ҳ��㴬�;�Ԯͧͬ��ʱ��E�������������ٲ��䣬��
���㴬�����������У���Ԯͧ�����ٴε���������CE����ǰȥ��Ԯ�����Ҳ��㴬�;�Ԯͧͬ��ʱ��E�������������ٲ��䣬��![]() ������ֵ��
������ֵ��![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���ܳ�Ϊ36 cm���Խ���
���ܳ�Ϊ36 cm���Խ���![]() �ཻ�ڵ�
�ཻ�ڵ�![]() cm������
cm������![]() ��
��![]() ���е㣬��
���е㣬��![]() ���ܳ�Ϊ�� ��
���ܳ�Ϊ�� ��
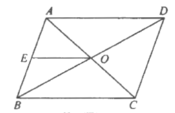
A.10 cmB.15 cmC.20 cmD.30 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.�˽���������֪��������������������������ʺ�ȫ����飻
B.�����������߳ɼ��ķ���ֱ�Ϊ![]() ��˵���ҵľ���ɼ��ȼ��ȶ���
��˵���ҵľ���ɼ��ȼ��ȶ���
C.һ������2��2��3��4��������2����λ����2.5��
D.��������1%���¼���һ��������һ�����ᷢ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com