
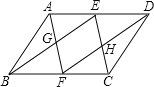
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当AB与BC满足什么条件时,四边形EGFH为矩形?并说明理由.
【答案】(1)证明见解析;(2)当BC=2AB时,平行四边形EGFH是矩形.理由见解析.
【解析】
(1)可分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,从而得出GF∥EH,GE∥FH,即可证明四边形EGFH是平行四边形;
(2)证出四边形ABFE是菱形,得出AF⊥BE,即∠EGF=90°,即可得出结论.
(1)连接EF,如图所示:
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC.
∵点E、F分别是AD、BC的中点,
∴AE=ED![]() AD,BF=FC
AD,BF=FC![]() BC,
BC,
∴AE//FC,AE=FC,
∴四边形AECF是平行四边形,
∴GF//EH.
同理可证:ED//BF且ED=BF,
∴四边形BFDE是平行四边形,
∴GE//FH,
∴四边形EGFH是平行四边形.
(2)当BC=2AB时,平行四边形EGFH是矩形.理由如下:
由(1)同理可证四边形ABFE是平行四边形,
当BC=2AB时,AB=BF,
∴四边形ABFE是菱形,
∴AF⊥BE,即∠EGF=90°,
∴平行四边形EGFH是矩形.


科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,点A是劣弧BC的中点,AD交BC于点E,连结AB.
(1)求证:AB2=AE·AD;
(2)若AE=2,ED=4,求图中阴影的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,直线
,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于点
的图象相交于点![]() 和点
和点![]() .
.

(1)求直线![]() 与反比例函数的解析式;
与反比例函数的解析式;
(2)求![]() 的度数;
的度数;
(3)将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角(
角(![]() 为锐角),得到
为锐角),得到![]() ,当
,当![]() 为多少度时
为多少度时![]() ,并求此时线段
,并求此时线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究如图,在正方形![]() 中,点
中,点![]() 在
在![]() 边所在的直线上运动但不与点
边所在的直线上运动但不与点![]() 重合,点
重合,点![]() 在线段
在线段![]() .上运动,过点
.上运动,过点![]() 的直线
的直线![]() ,分别交
,分别交![]() 于点
于点![]() .
.
观察探究:(1)如图1,当点![]() 在边
在边![]() 上时,判断并说明
上时,判断并说明![]() 与
与![]() 的数量关系;
的数量关系;
探究发现:(2)勤奋小组在图1的基础上得到图2,点![]() 为
为![]() 中点时,其他条件不变,连接正方形的对角线
中点时,其他条件不变,连接正方形的对角线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,此时,
,此时,![]() ,请利用图2证明;
,请利用图2证明;
探究拓展:(3)如图3,缜密小组在勤奋小组的启发下,当点![]() 在点
在点![]() 右侧时,如果(2)中的其他条件不变,直线
右侧时,如果(2)中的其他条件不变,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,他们发现线段
,他们发现线段![]() 与
与![]() 之间存在数量关系,线段
之间存在数量关系,线段![]() 与
与![]() 之间也存在数量关系,请你直接写出.
之间也存在数量关系,请你直接写出.
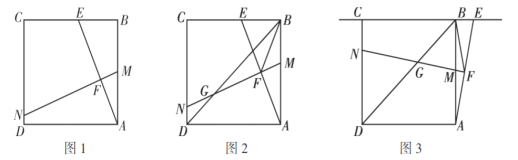
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
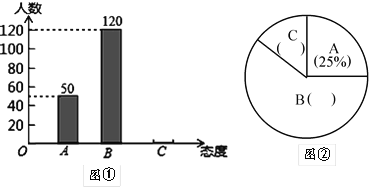
(1)此次抽样调査中.共调査了______名中学生家长;
(2)将图形①、②补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)求证:直线CD是⊙O的切线;
(2)若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 经过原点
经过原点![]() ,
,![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)如图2,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,作
,作![]() ,连接
,连接![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西汾酒,又称“杏花村酒”.酿造汾酒是选用晋中平原的“一把抓高粱”为原料.汾阳县某村民合作社2016年种植“一把抓高粱”100亩,2018年该合作社扩大了“一把抓高梁”的种植面积,共种植144亩.
(1)求该合作社这两年种植“一把抓高梁”亩数的平均增长率;
(2)某粮店销售“一把抓高粱”售价为13元/斤,每天可售出30斤,每斤的盈利是1.5元.为了减少库存,粮店决定搞促销活动.在销售中发现:售价每降价0.1元,则可多售出2斤.若该粮店某天销售“一把抓高梁”的盈利为40元,则该店当天销售单价降低了多少元?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com