
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈ2ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ![]() ЃЉЃЌЕуOЃЈ0ЃЌ0ЃЉЃЎЁїAOBШЦзХOЫГЪБеыа§зЊЃЌЕУЁїA'OB'ЃЌЕуAЁЂBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЎ
ЃЉЃЌЕуOЃЈ0ЃЌ0ЃЉЃЎЁїAOBШЦзХOЫГЪБеыа§зЊЃЌЕУЁїA'OB'ЃЌЕуAЁЂBа§зЊКѓЕФЖдгІЕуЮЊA'ЃЌB'ЃЌМЧа§зЊНЧЮЊІСЃЎ
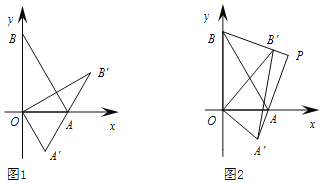
ЃЈЂёЃЉШчЭМ1ЃЌA'B'ЧЁКУОЙ§ЕуAЪБЃЌЧѓДЫЪБа§зЊНЧІСЕФЖШЪ§ЃЌВЂЧѓГіЕуB'ЕФзјБъЃЛ
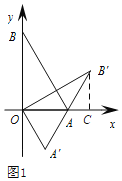
ЃЈЂђЃЉШчЭМ2ЃЌШє0ЁуЃМІСЃМ90ЁуЃЌЩшжБЯпAA'КЭжБЯпBB'НЛгкЕуPЃЌЧѓжЄЃКAA'ЁЭBB'ЃЛ
ЃЈЂѓЃЉШє0ЁуЃМІСЃМ360ЁуЃЌЧѓЃЈЂђЃЉжаЕФЕуPзнзјБъЕФзюаЁжЕЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ
ЁОД№АИЁПЃЈЂёЃЉІСЃН60ЁуЃЌB'ЃЈ3ЃЌ![]() ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ
ЃЉЃЛЃЈЂђЃЉМћНтЮіЃЛЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2ЃЎ
Љ2ЃЎ
ЁОНтЮіЁП
ЃЈЂёЃЉзїИЈжњЯп,ЯШИљОнЕуAЃЈ2,0ЃЉ,ЕуBЃЈ0,![]() ЃЉ,ШЗЖЈЁЯABOЃН30Ёу,жЄУїЁїAOA'ЪЧЕШБпШ§НЧаЮ,ЕУа§зЊНЧІСЃН60Ёу,жЄУїЁїCOB'ЪЧ30ЁуЕФжБНЧШ§НЧаЮ,ПЩЕУB'ЕФзјБъ;
ЃЉ,ШЗЖЈЁЯABOЃН30Ёу,жЄУїЁїAOA'ЪЧЕШБпШ§НЧаЮ,ЕУа§зЊНЧІСЃН60Ёу,жЄУїЁїCOB'ЪЧ30ЁуЕФжБНЧШ§НЧаЮ,ПЩЕУB'ЕФзјБъ;
ЃЈЂђЃЉвРОна§зЊЕФаджЪПЩЕУЁЯBOB'ЃНЁЯAOA'ЃНІС,OBЃНOB',OAЃНOA',МДПЩЕУГіЁЯOBB'ЃНЁЯOA'AЃН![]() ЃЈ180ЁуЉІСЃЉ,дйИљОнЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,МДПЩЕУЕНЁЯBPA'ЃН90Ёу,МДAA'ЁЭBB';
ЃЈ180ЁуЉІСЃЉ,дйИљОнЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,МДПЩЕУЕНЁЯBPA'ЃН90Ёу,МДAA'ЁЭBB';
ЃЈЂѓЃЉзїABЕФжаЕуMЃЈ1,![]() ЃЉ,СЌНгMP,вРОнЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН
ЃЉ,СЌНгMP,вРОнЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН![]() ABЃН2ЮЊАыОЖЕФдВ,МДПЩЕУЕНЕБPMЁЮyжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ
ABЃН2ЮЊАыОЖЕФдВ,МДПЩЕУЕНЕБPMЁЮyжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2.
Љ2.
НтЃКЃЈЂёЃЉШчЭМ1ЃЌЙ§B'зїB'CЁЭxжсгкC,
ЁпOAЃН2,OBЃН2![]() ,ЁЯAOBЃН90Ёу,
,ЁЯAOBЃН90Ёу,
ЁрЁЯABOЃН30Ёу,ЁЯBAOЃН60Ёу,
гЩа§зЊЕУЃКOAЃНOA',ЁЯA'ЃНЁЯBAOЃН60Ёу,
ЁрЁїOAA'ЪЧЕШБпШ§НЧаЮ,
ЁрІСЃНЁЯAOA'ЃН60Ёу,
ЁпOBЃНOB'ЃН2![]() ,ЁЯCOB'ЃН90ЁуЉ60ЁуЃН30Ёу,
,ЁЯCOB'ЃН90ЁуЉ60ЁуЃН30Ёу,
ЁрB'CЃН![]() OBЁЏЃН
OBЁЏЃН![]() ,
,
ЁрOCЃН3,
ЁрB'ЃЈ3,![]() ЃЉ,
ЃЉ,
ЃЈЂђЃЉжЄУїЃКШчЭМ2,ЁпЁЯBOB'ЃНЁЯAOA'ЃНІС,OBЃНOB',OAЃНOA',
ЁрЁЯOBB'ЃНЁЯOA'AЃН![]() ЃЈ180ЁуЉІСЃЉ,
ЃЈ180ЁуЉІСЃЉ,
ЁпЁЯBOA'ЃН90Ёу+ІС,ЫФБпаЮOBPA'ЕФФкНЧКЭЮЊ360Ёу,
ЁрЁЯBPA'ЃН360ЁуЉЃЈ180ЁуЉІСЃЉЉЃЈ90Ёу+ІСЃЉЃН90Ёу,
МДAA'ЁЭBB';
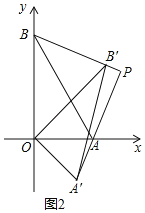
ЃЈЂѓЃЉЕуPзнзјБъЕФзюаЁжЕЮЊ![]() -2ЃЎРэгЩЪЧЃК
-2ЃЎРэгЩЪЧЃК
ШчЭМЃЌзїABЕФжаЕуMЃЈ1,![]() ЃЉ,СЌНгMP,
ЃЉ,СЌНгMP,

ЁпЁЯAPBЃН90Ёу,
ЁрЕуPЕФЙьМЃЮЊвдЕуMЮЊдВаФ,вдMPЃН![]() ABЃН2ЮЊАыОЖЕФдВ,Г§ШЅЕуЃЈ2,2
ABЃН2ЮЊАыОЖЕФдВ,Г§ШЅЕуЃЈ2,2![]() ЃЉ,
ЃЉ,
ЁрЕБPMЁЭxжсЪБ,ЕуPзнзјБъЕФзюаЁжЕЮЊ![]() Љ2ЃЎ
Љ2ЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() НЛ
НЛ![]() жсЕФИКАыжсгкЕу
жсЕФИКАыжсгкЕу![]() .Еу
.Еу![]() ЪЧ
ЪЧ![]() жсе§АыжсЩЯвЛЕуЃЌЕу
жсе§АыжсЩЯвЛЕуЃЌЕу![]() ЙигкЕу
ЙигкЕу![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЧЁКУТфдкХзЮяЯпЩЯ.Й§Еу
ЧЁКУТфдкХзЮяЯпЩЯ.Й§Еу![]() зї
зї![]() жсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕу
жсЕФЦНааЯпНЛХзЮяЯпгкСэвЛЕу![]() .ШєЕу
.ШєЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ________.
ЕФГЄЮЊ________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋЁїABCЗХдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌЕуAЁЂBЁЂCОљТфдкИёЕуЩЯЃЎ
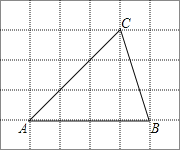
ЃЈ1ЃЉЁїABCЕФУцЛ§ЕШгкЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉШєЫФБпаЮDEFGЪЧЁїABCжаЫљФмАќКЌЕФУцЛ§зюДѓЕФе§ЗНаЮЃЌЧыФудкШчЭМЫљЪОЕФЭјИёжаЃЌгУжБГпКЭШ§НЧГпЛГіИУе§ЗНаЮЃЌВЂМђвЊЫЕУїЛЭМЗНЗЈЃЈВЛвЊЧѓжЄУїЃЉЁЁЁЁЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
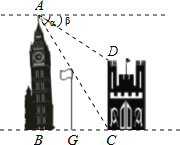
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкСННЈжўЮяжЎМфгавЛИпЮЊ15УзЕФЦьИЫЃЌДгИпНЈжўЮяЕФЖЅЖЫAЕуОЙ§ЦьИЫЖЅЕуЧЁКУПДЕНАЋНЈжўЮяЕФЕзЖЫЧННЧCЕуЃЌЧвИЉНЧaЮЊ60ЁуЃЌгжДгAЕуВтЕУАЋНЈжўЮязѓЩЯНЧЖЅЖЫDЕуЕФИЉНЧІТЮЊ30ЁуЃЌШєЦьИЫЕзВПЕуGЮЊBCЕФжаЕуЃЈЕуBЮЊЕуAЯђЕиУцЫљзїДЙЯпЕФДЙзуЃЉдђАЋНЈжўЮяЕФИпCDЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШ№АВЪаВмДхеђЁААЫАйФъЕЦЛсЁБГЩЮЊЮТжнЁАЩъвХЁБЕФБІЙѓЯюФПЃЎФГЙЋЫОЩњВњСЫвЛжжМЭФюЛЈЕЦЃЌУПМўМЭФюЛЈЕЦжЦдьГЩБОЮЊ18дЊЃЎЩшЯњЪлЕЅМлxЃЈдЊЃЉЃЌУПШеЯњЪлСПyЃЈМўЃЉУПШеЕФРћШѓwЃЈдЊЃЉЃЎдкЪдЯњЙ§ГЬжаЃЌУПШеЯњЪлСПyЃЈМўЃЉЁЂУПШеЕФРћШѓwЃЈдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфДцдквЛЖЈЕФЙиЯЕЃЌЦфМИзщЖдгІСПШчЯТБэЫљЪОЃК
ЃЈдЊЃЉ | 19 | 20 | 21 | 30 |
ЃЈМўЃЉ | 62 | 60 | 58 | 40 |
ЃЈ1ЃЉИљОнБэжаЪ§ОнЕФЙцТЩЃЌЗжБ№аДГіАШеЯњЪлСПyЃЈМўЃЉЃЌУПШеЕФРћШѓwЃЈдЊЃЉЙигкЯњЪлЕЅМлxЃЈдЊЃЉжЎМфЕФКЏЪ§БэДяЪНЃЎЃЈРћШѓЃНЃЈЯњЪлЕЅМлЉГЩБОЕЅМлЃЉЁСЯњЪлМўЪ§ЃЉЃЎ
ЃЈ2ЃЉЕБЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌЙЋЫОУПШеФмЙЛЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИљОнЮяМлОжЙцЖЈЃЌетжжМЭФюЦЗЕФЯњЪлЕЅМлВЛЕУИпгк32дЊЃЌШчЙћЙЋЫОвЊЛёЕУУПШеВЛЕЭгк350дЊЕФРћШѓЃЌФЧУДжЦдьетжжМЭФюЛЈЕЦУПШеЕФзюЕЭжЦдьГЩБОашвЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧЁїABCЕФЭтНгдВЃЌЕуOдкBCБпЩЯЃЌЁЯBACЕФЦНЗжЯпНЛЁбOгкЕуDЃЌСЌНгBDЁЂCDЃЌЙ§ЕуDзїBCЕФЦНааЯпгыACЕФбгГЄЯпЯрНЛгкЕуPЃЎ
ЃЈ1ЃЉЧѓжЄЃКPDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїABDЁзЁїDCPЃЛ
ЃЈ3ЃЉЕБAB=5cmЃЌAC=12cmЪБЃЌЧѓЯпЖЮPCЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌбЇаЃЕФЪЕбщТЅЖдУцЪЧвЛДБНЬбЇТЅЃЌаЁУєдкЪЕбщТЅЕФДАПкCДІВтЕУНЬбЇТЅЖЅВПDДІЕФбіНЧЮЊ18ЁуЃЌНЬбЇТЅЕзВПBДІЕФИЉНЧЮЊ20ЁуЃЌНЬбЇТЅЕФИпBD=21mЃЌЧѓЪЕбщТЅгыНЬбЇТЅжЎМфЕФОрРыABЃЈНсЙћБЃСєећЪ§ЃЉЃЎЃЈВЮПМЪ§ОнЃКtan18ЁуЁж0.32ЃЌtan20ЁуЁж0.36ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
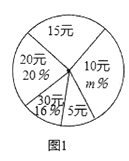
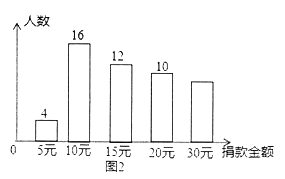
ЁОЬтФПЁПЮЊСЫАяжњЦЖРЇСєЪиЖљЭЏЃЌКыбяЗіЦЖМУРЇЕФДЋЭГУРЕТЃЌФГаЃЭХЮЏдкбЇаЃОйааЁАЫЭЮТХЏЃЌЯзАЎаФЁБОшПюЛюЖЏЃЌШЋаЃ2000УћбЇЩњЖМЛ§МЋВЮгыСЫИУДЮЛюЖЏ.ЮЊСЫНтОшПюЧщПіЃЌЫцЛњЕїВщСЫИУаЃВПЗжбЇЩњЕФОшПюН№ЖюЃЌВЂгУЕУЕНЕФЪ§ОнЛцжЦГіШчЯТЭГМЦЭМ1КЭЭМ2ЃЌЧыИљОнЯрЙиаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈIЃЉБОДЮНгЪмЫцЛњГщбљЕїВщЕФбЇЩњШЫЪ§ЮЊ_________________ЃЌЭМ1жаmЕФжЕЪЧ_________________.
ЃЈЂђЃЉЧѓБОДЮЕїВщЛёШЁЕФбљБОЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂѓЃЉИљОнбљБОЪ§ОнЃЌЙРМЦИУаЃБОДЮЛюЖЏОшПюН№ЖюГЌЙ§20дЊЕФбЇЩњШЫЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+cЕФЖЅЕуЮЊDЃЈЉ1ЃЌ2ЃЉЃЌгыxжсЕФвЛИіНЛЕуAдкЕуЃЈЉ3ЃЌ0ЃЉКЭЃЈЉ2ЃЌ0ЃЉжЎМфЃЌЦфВПЗжЭМЯѓШчЭМЃЌдђвдЯТНсТлЃКЂйb2Љ4acЃМ0ЃЛЂкa+b+cЃМ0ЃЛЂлcЉa=2ЃЛЂмЗНГЬax2+bx+cЉ2=0гаСНИіЯрЕШЕФЪЕЪ§ИљЃЎЦфжае§ШЗНсТлЕФИіЪ§ЮЊЃЈЁЁЁЁЃЉ
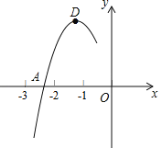
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com