
【题目】为了帮助贫困留守儿童,弘扬扶贫济困的传统美德,某校团委在学校举行“送温暖,献爱心”捐款活动,全校2000名学生都积极参与了该次活动.为了解捐款情况,随机调查了该校部分学生的捐款金额,并用得到的数据绘制出如下统计图1和图2,请根据相关信息,解答下列问题:
(I)本次接受随机抽样调查的学生人数为_________________,图1中m的值是_________________.
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额超过20元的学生人数.
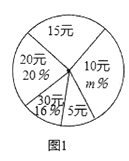
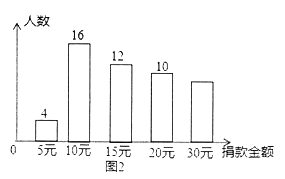
【答案】(I)50,32;(II)平均数为16,众数为10,中位数为15;(III)估计该校捐款20元以上的学生约有320人
【解析】
(1)根据捐款20元的具体人数除以其对应的比例,可求出总数.再用10元的人数除以总人数即可得到m.
(2)平均数=![]() ,捐款人数最多的金额即为众数,将捐款的金额从小到大排列最中间的就是中位数;
,捐款人数最多的金额即为众数,将捐款的金额从小到大排列最中间的就是中位数;
(3)用总人数乘以样本中“捐款金额超过20元的学生”人数所占百分比可得 .
解:(1)10÷20%=50,
![]() ,故m=32.
,故m=32.
(Ⅱ)捐30元的人数为:![]()
![]()
∴这组样本数据的平均数为16
∵在这组样本数据中,10出现了16次,出现次数最多,
∴这组样本数据的众数为10
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是15,
有![]()
∴这组样本数据的中位数为15
(III)∵捐款20元以上的学生占![]()
∴捐款20元以上的学生人数是:![]()
答:估计该校捐款20元以上的学生约有320人.


科目:初中数学 来源: 题型:
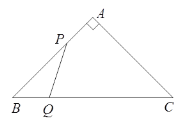
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(2,0),点B(0,![]() ),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
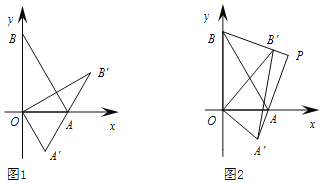
(Ⅰ)如图1,A'B'恰好经过点A时,求此时旋转角α的度数,并求出点B'的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';
(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车和一辆快车沿相同路线从A地到B地,所行驶的路程与时间的函数图象如图所示,下列说法正确的有()个
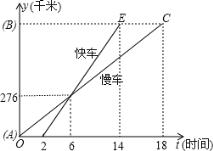
①快车追上慢车需6小时
②慢车比快车早出发2小时
③快车速度为46km/h
④慢车速度为46km/h
⑤AB两地相距828km
⑥快车14小时到达B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
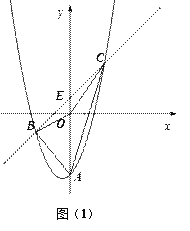
【题目】如图(1),抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C .
与抛物线交于点B、C .
(1)则点A的坐标是 ______ ;
(2)当b = 0时(如图(2)),△ABE与△ACE的面积大小关系如何?当![]() 时,上述关系还成立吗,为什么?
时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC 为斜边的直角三角形,若存在,求出b;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com