
【题目】已知![]() 在半径为1的
在半径为1的![]() 上,直线
上,直线![]() 与
与![]() 相切,
相切,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
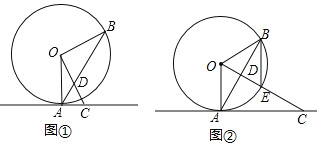
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() -1.
-1.
【解析】
(1)由切线的性质可知∠OAC=90°,由三角形的内角和定理可知∠AOC=30°,由∠AOB=∠AOC+∠BOC可得出∠AOB的度数,结合OA=OB可得出∠OAB=∠OBA=30°,由此可得出OD=AD,由∠OAB与∠DAC互余可知∠DAC=60°=∠DCA,由此得出△DAC为等边三角形,从而得出OD=AC,由特殊角的三角函数值即可得出结论;
(2)由OC⊥OB且OC=OB可知∠OBE=∠OEB=45°,再由BE∥OA可得出∠AOC=45°,结合切线性质可得出OA=AC,根据角与角之间的关系逐步得出∠CAD=∠CDA=67.5°,由此可得出AC=CD,结合勾股定理即可得出结论.
解:(1)∵AC与⊙O相切,
∴∠OAC=90°.
∵∠OCA=60°,
∴∠AOC=30°.
∵OC⊥OB,
∴∠AOB=∠AOC+∠BOC=120°.
∵OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=AD,∠DAC=60°
∴AD=CD=AC.
∵OA=1,
∴OD=AC=OAtan∠AOC=![]() .
.
(2)∵OC⊥OB,
∴∠OBE=∠OEB=45°.
∵BE∥OA,
∴∠AOC=45°,∠ABE=∠OAB,
∴OA=AC,∠OAB=∠OBA=22.5°,
∴∠ADC=∠AOC+∠OAB=67.5°.
∵∠DAC=90°-∠OAB=67.5°=∠ADC,
∴AC=CD.
∵OC=![]() =
=![]() ,
,
∴OD=OC-CD=![]() -1.
-1.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
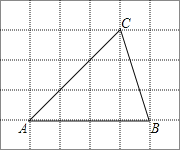
(1)△ABC的面积等于 ;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

查看答案和解析>>
科目:初中数学 来源: 题型:
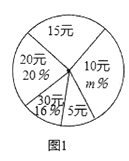
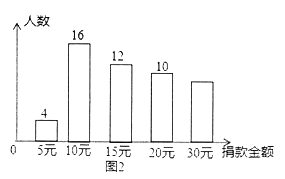
【题目】为了帮助贫困留守儿童,弘扬扶贫济困的传统美德,某校团委在学校举行“送温暖,献爱心”捐款活动,全校2000名学生都积极参与了该次活动.为了解捐款情况,随机调查了该校部分学生的捐款金额,并用得到的数据绘制出如下统计图1和图2,请根据相关信息,解答下列问题:
(I)本次接受随机抽样调查的学生人数为_________________,图1中m的值是_________________.
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额超过20元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
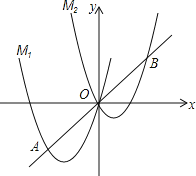
【题目】如图,将抛物线M1:y=ax2+4x向右平移3个单位,再向上平移3个单位,得到抛物线M2,直线y=x与M1的一个交点记为A,与M2的一个交点记为B,点A的横坐标是﹣3.
(1)求a的值及M2的表达式;
(2)点C是线段AB上的一个动点,过点C作x轴的垂线,垂足为D,在CD的右侧作正方形CDEF.
①当点C的横坐标为2时,直线y=x+n恰好经过正方形CDEF的顶点F,求此时n的值;
②在点C的运动过程中,若直线y=x+n与正方形CDEF始终没有公共点,求n的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
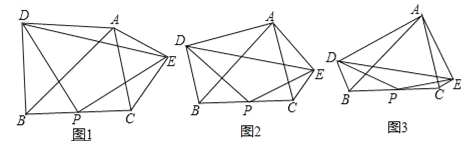
【题目】已知在△ABC中,∠BAC=60°,点P为边BC的中点,分别以AB和AC为斜边向外作Rt△ABD和Rt△ACE,且∠DAB=∠EAC=α,连结PD,PE,DE.
(1)如图1,若α=45°,则![]() = ;
= ;
(2)如图2,若α为任意角度,求证:∠PDE=α;
(3)如图3,若α=15°,AB=8,AC=6,则△PDE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )
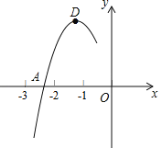
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com