
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.
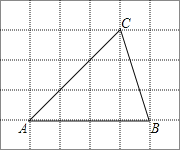
(1)△ABC的面积等于 ;
(2)若四边形DEFG是△ABC中所能包含的面积最大的正方形,请你在如图所示的网格中,用直尺和三角尺画出该正方形,并简要说明画图方法(不要求证明) .
科目:初中数学 来源: 题型:
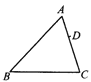
【题目】如图,在△ABC中,AB=24,AC=18,D是AC上一点,AD=6,在AB上取一点E,使A、D、E三点组成的三角形与△ABC相似,则AE的长为( )
A.8B.![]() C.8或
C.8或![]() D.8或9
D.8或9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人“五一”放假期间去登盘山挂月峰,甲先开车沿小路开到了距离登山入口100米的地方后,开始以10米/分钟的登山上升速度徒步登山;甲开始徒步登山同时,乙直接从登山入口开始徒步登山,起初乙以15米/分钟的登山上升速度登山,两分钟后得知甲已经在半山腰,于是乙以甲登山上升速度的3倍提速.两人相约只登到距地面高度为300米的地方,设两人徒步登山时间为![]() (分钟)
(分钟)
(Ⅰ)根据题意,填写下表:
徒步登山时间/时间 | 2 | 3 | 4 | 5 | … |
甲距地面高度/米 | 120 | ______ | 140 | ______ | … |
乙距地面高度/米 | 30 | 60 | ______ | ______ | … |
(Ⅱ)请分别求出甲、乙两人徒步登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式;
(分)之间的函数关系式;
(Ⅲ)登山多长时间时,甲、乙两人距地面的高度差为70米?
查看答案和解析>>
科目:初中数学 来源: 题型:
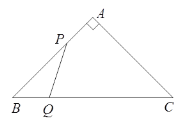
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
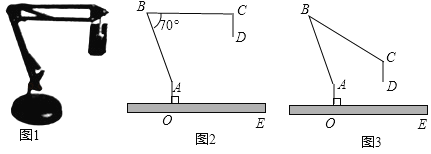
【题目】图1是一台实物投影仪,图2是它的示意图,折线![]() 表示固定支架,
表示固定支架,![]() 垂直水平桌面
垂直水平桌面![]() 于点
于点![]() ,点
,点![]() 为旋转点,
为旋转点,![]() 可转动,当
可转动,当![]() 绕点
绕点![]() 顺时针旋转时,投影探头
顺时针旋转时,投影探头![]() 始终垂直于水平桌面
始终垂直于水平桌面![]() ,经测量:
,经测量:![]() ,
,![]() ,
,![]() ,
,![]() .(结果精确到0.1)
.(结果精确到0.1)
(1)如图2,![]() ,
,![]() .
.
①填空:![]() _________°;
_________°;
②求投影探头的端点![]() 到桌面
到桌面![]() 的距离.
的距离.
(2)如图3,将(1)中的![]() 向下旋转,当投影探头的端点
向下旋转,当投影探头的端点![]() 到桌面
到桌面![]() 的距离为
的距离为![]() 时,求
时,求![]() 的大小.(参考数据:
的大小.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(2,0),点B(0,![]() ),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
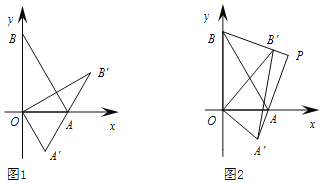
(Ⅰ)如图1,A'B'恰好经过点A时,求此时旋转角α的度数,并求出点B'的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';
(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com