
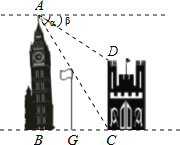
【题目】如图所示,在两建筑物之间有一高为15米的旗杆,从高建筑物的顶端A点经过旗杆顶点恰好看到矮建筑物的底端墙角C点,且俯角a为60°,又从A点测得矮建筑物左上角顶端D点的俯角β为30°,若旗杆底部点G为BC的中点(点B为点A向地面所作垂线的垂足)则矮建筑物的高CD为_____.
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
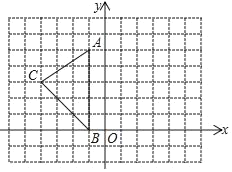
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3)
(1)将△ABC向右平移6个单位至△A1B1C1,再将△A1B1C1绕点E(5,1)逆时针旋转90°至△A2B2C2,请按要求画出图形;
(2)在(1)的变换过程中,直接写出点C的运动路径长
(3)△A2B2C2可看成△ABC绕某点P旋转90°得到的,则点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
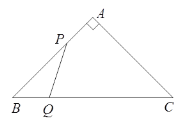
【题目】如图,△ABC是直角边长为1cm的等腰直角三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t(s),解答下列各问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的二分之一?如果存在,求出t的值;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买某种树苗绿化校园,甲、乙两林场这种树苗的售价都是每棵20元,又各有不同的优惠方案,甲林场:若一次购买20棵以上,售价是每棵18元;乙林场:若一次购买10棵以上,超过10棵部分打8.5折。设学校一次购买这种树苗x棵(x是正整数).
(Ⅰ)根据题意填写下表:
学校一次购买树苗(棵) | 10 | 15 | 20 | 40 |
在甲林场实际花费(元) | 200 | 300 | ||
在乙林场实际花费(元) | 200 | 370 | 710 |
(Ⅱ)学校在甲林场一次购买树苗,实际花费记为![]() (元),在乙林场一次购买树苗,实际花费记为
(元),在乙林场一次购买树苗,实际花费记为![]() (元),请分别写出
(元),请分别写出![]() 与x的函数关系式;
与x的函数关系式;
(Ⅲ)当![]() 时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
时,学校在哪个林场一次购买树苗,实际花费较少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,过点A作半圆O的切线交BC的延长线于点F,连结BE,AD
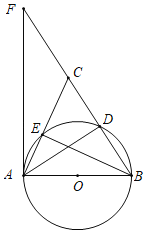
(1)求证:∠F=∠EBC;
(2)若AE=2,tan∠EAD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A(2,0),点B(0,![]() ),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
),点O(0,0).△AOB绕着O顺时针旋转,得△A'OB',点A、B旋转后的对应点为A',B',记旋转角为α.
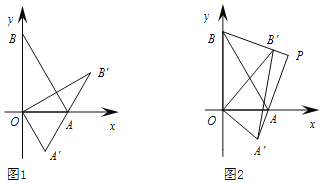
(Ⅰ)如图1,A'B'恰好经过点A时,求此时旋转角α的度数,并求出点B'的坐标;
(Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P,求证:AA'⊥BB';
(Ⅲ)若0°<α<360°,求(Ⅱ)中的点P纵坐标的最小值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
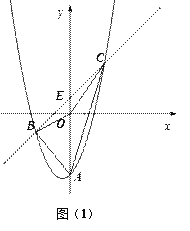
【题目】如图(1),抛物线![]() 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线![]() 与抛物线交于点B、C .
与抛物线交于点B、C .
(1)则点A的坐标是 ______ ;
(2)当b = 0时(如图(2)),△ABE与△ACE的面积大小关系如何?当![]() 时,上述关系还成立吗,为什么?
时,上述关系还成立吗,为什么?
(3)是否存在这样的b,使得△BOC是以BC 为斜边的直角三角形,若存在,求出b;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com