
【题目】如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB=![]() .
.
(1)则 A、B 两点的坐标分别为 A( , ); B( , );
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为 .

【答案】(1)﹣1,0;3,0;(2)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;(3)(1,﹣
;(3)(1,﹣![]() )
)
【解析】
(1)先求得抛物线的对称轴为x=1,然后利用平行线分线段成比例定理求得OE:EB的值,从而得到点B的坐标,利用抛物线的对称性可求得点A的坐标;
(2)过点C作CF⊥PE,垂足为F.先求得点C和点P的坐标(用含字母的式子表示),然后可得到PF=a,然后利用锐角三角函数的定义可求得a的值,然后将点A和点B的坐标代入抛物线的解析式可求得c的值;
(3)根据三角形的任意两边之差小于第三边判断出点A、C、M在同一直线上时|MC-MB|最大,设直线AC的解析式为y=kx+b,利用待定系数法求出一次函数解析式,再根据点M在对称轴上代入计算即可得解.
(1)如图所示:
∵由题意可知:抛物线的对称轴为x=1,
∴OE=1.
∵OC∥PE∥BD,CP:PD=1:2,
∴![]() =
=![]() .
.
∴BE=2.
∴OB=3.
∴B(3,0).
∵点A与点B关于PE对称,
∴点A的坐标为(﹣1,0).
故答案是:﹣1,0;3,0;
(2)过点C作CF⊥PE,垂足为F.
将x=0代入得:y=c,
∴点C的坐标为(0,c).
将x=1代入得y=﹣a+c.
∴点P的坐标为(1,﹣a+c).
∴PF=a.
∵PE∥BD,tan∠PDB=![]() ,
,
∴tan∠CPF=tan∠PDB=![]() .
.
∴![]() .
.
解得a=![]() .
.
将a=![]() 代入抛物线的解析式得:y=
代入抛物线的解析式得:y=![]() x2﹣
x2﹣![]() x+c.
x+c.
将点A的坐标代入得:![]() +
+![]() +c=0,解得:c=﹣
+c=0,解得:c=﹣![]() .
.
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() .
.
(3)由三角形的三边关系,|MC﹣MB|<AC,
∴当点A、C、M在同一直线上时|MC﹣MB|最大,
设直线AC的解析式为y=kx+b,
则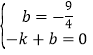 ,
,
解得 ,
,
∴y=﹣![]() x﹣
x﹣![]() ,
,
∵抛物线对称轴为直线x=1,
∴当x=1时,y=﹣![]() ×1﹣
×1﹣![]() =﹣
=﹣![]() ,
,
∴点M的坐标为(1,﹣![]() ).
).
故答案是:(1,﹣![]() ).
).


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点E在AB上,点F在BC的延长线上,将正方形ABCD沿直线EF翻折,使点B刚好落在AD边上的点G处,连接GF交CD于点H,连接BH,若AG=4,DH=6,则BH=_____.
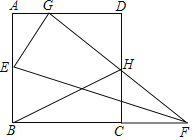
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆 O 的半径为 1,过点 A(2,0)的直线与圆 O 相切于点 B,与 y 轴相交于点 C.
(1)求 AB 的长;
(2)求直线 AB 的解析式.
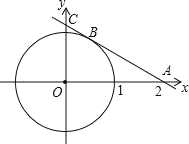
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球 3 个、黄球 1 个,这些球除颜色外都相同,均匀摇匀.
(1)从布袋中一次摸出 1 个球,计算“摸出的球恰是黄球”的概率;
(2)从布袋中一次摸出 2 个球,计算“摸出的球恰是一红一黄”的概率(用“ 画树状图”或“列表”的方法写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中.
中.
![]() 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离![]() 的长
的长![]() 等于PC的长;
等于PC的长;
![]() 利用尺规作图,作出
利用尺规作图,作出![]() 中的线段PD.
中的线段PD.
![]() 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
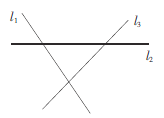
A.一处B.二处C.三处D.四处
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com