
如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=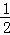 ∠BAC,则tan∠BPC= .
∠BAC,则tan∠BPC= .
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
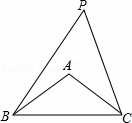
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点且AE:EB=4:1,EF⊥AC于F,连接FB,则tan∠CFB的值等于( )
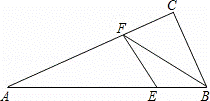
A. 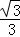 B.
B.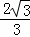 C.
C.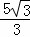 D.
D. 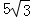
查看答案和解析>>
科目:初中数学 来源: 题型:
如果三角形满足一个角是另一个角的3倍,那么我们称这个三角形为“智慧三角形”.下列各组数据中,能作为一个智慧三角形三边长的一组是( )
A. 1,2,3 B.1,1,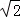 C.1,1,
C.1,1,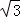 D. 1,2,
D. 1,2,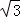
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
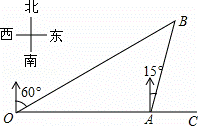
A. 4km B.2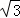 km C.2
km C.2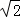 km D. (
km D. (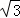 +1)km
+1)km
查看答案和解析>>
科目:初中数学 来源: 题型:
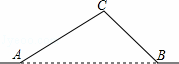
如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°,因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直的公路AB的长;
(2)问公路改直后比原来缩短了多少千米?(s in25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
in25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com