
【题目】2019年全国两会于3月5日在人民大会堂开幕,某社区为了解居民对此次两会的关注程度,在全社区范围内随机抽取部分居民进行问卷调查,根据调查结果,把居民对两会的关注程度分成“淡薄”、“一般”、“较强”、“很强”四个层次,并绘制成如下不完整的统计图:


请结合图表中的信息,解答下列问题:
(1)此次调查一共随机抽取了_____名居民;
(2)请将条形统计图补充完整;
(3)扇形统计图中,“很强”所对应扇形圆心角的度数为_____;
(4)若该社区有1500人,则可以估计该社区居民对两会的关注程度为“淡薄”层次的约有 _____人.
【答案】(1)120;(2)详见解析;(3)108°;(4)150
【解析】
(1)根据安全意识一般的有18人,所占的百分比是15%,据此即可求得调查的总人数,
(2)求出安全意识较强的人数,补全统计图即可.
(3)然后利用百分比的意义求得安全意识为“很强”的居民占被调查居民总数的百分比;用![]() 乘以其所占的百分比即可.
乘以其所占的百分比即可.
(4)利用总人数乘以对应的百分比即可求解;
(1)这次调查的居民总数为:18÷15%=120(名);
(2) 关注程度为“较强”的人数是:120×45%=54(名),补全的条形统计图为:
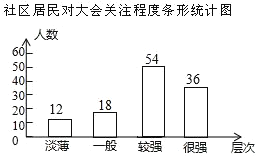
(3) 关注程度为“很强”的居民占被调查居民总数的百分比是:![]()
“很强”所对应扇形圆心角的度数为:![]()
(4)对两会的关注程度为“淡薄”层次的约有![]()


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
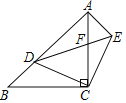
【题目】如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CFCA;④若AB=3![]() ,AD=2BD,则AF=
,AD=2BD,则AF=![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——应用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移的方法画出一个函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:
在函数![]() 中,当
中,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
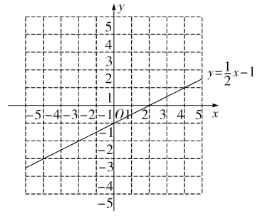
(1)求这个函数的表达式;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质;
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点的坐标分别为(8,0),(0,8),点
两点的坐标分别为(8,0),(0,8),点![]() ,
,![]() 分别是直线
分别是直线![]() 和
和![]() 轴上的动点,
轴上的动点,![]() ,点
,点![]() 是线段
是线段![]() 的中点,连接
的中点,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 面积取得最小值时,
面积取得最小值时,![]() 的值是( )
的值是( )
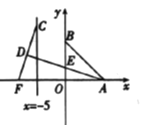
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
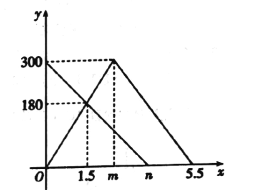
【题目】甲、乙两车分别从![]() 两地同时出发,甲车匀速前往
两地同时出发,甲车匀速前往![]() 地,到达
地,到达![]() 地立即以另一速度按原路匀速返回到
地立即以另一速度按原路匀速返回到![]() 地,乙车匀速前往
地,乙车匀速前往![]() 地.设甲、乙两车距
地.设甲、乙两车距![]() 地的路程为
地的路程为![]() (千米),甲车行驶的时间为
(千米),甲车行驶的时间为![]() (小时),
(小时),![]() 与
与![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)图中,![]() ,
,![]() ;
;
(2)求甲车返回时![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在甲车返回到![]() 地的过程中,当
地的过程中,当![]() 为何值时,甲、乙两车相距190千米?
为何值时,甲、乙两车相距190千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
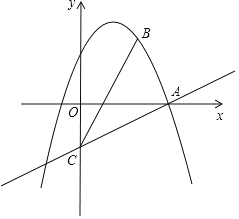
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com