
【题目】某公司开发出一款新的节能产品,该产品的成本价为8元/件,该产品在正式投放市场前通过代销点进行了为期一个月30天的试销售,售价为13元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成如图所示的图象,图中的折线![]() 表示日销量
表示日销量![]() (件)与销售时间
(件)与销售时间![]() (天)之间的函数关系.
(天)之间的函数关系.
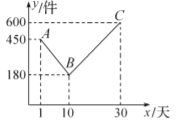
(1)直接写出![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围.
的取值范围.
(2)若该节能产品的日销售利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数解析式.日销售利润不超过1950元的共有多少天?
之间的函数解析式.日销售利润不超过1950元的共有多少天?
(3)若![]() ,求第几天的日销售利润最大,最大的日销售利润是多少元?
,求第几天的日销售利润最大,最大的日销售利润是多少元?
【答案】(1)![]() ;(2)
;(2)![]() ,18;(3)第5日的销售利润最大,最大销售利润为1650元.
,18;(3)第5日的销售利润最大,最大销售利润为1650元.
【解析】
(1)根据题意和函数图象中的数据,可利用待定系数法求得y与x的函数关系式,并写出x的取值范围;
(2)根据题意和(1)中的函数关系式可以写出w与x的函数关系式,求得日销售利润不超过1950元的天数;
(3)根据题意和(2)中的关系式分别求出当![]() 时和当
时和当![]() 时的最大利润,问题得解.
时的最大利润,问题得解.
(1)当1≤x≤10时,设y与x的函数关系式为y=kx+b,
则![]() ,解得:
,解得:![]() ,
,
即当1≤x≤10时,y与x的函数关系式为y=30x+480,
当10<x≤30时,设y与x的函数关系式为y=mx+n,
则![]() ,解得:
,解得:![]()
即当10<x≤30时,y与x的函数关系式为y=21x30,
综上可得, ![]() ;
;
(2)由题意可得:![]()
令![]() ,解得
,解得![]() .
.
令![]() ,解得
,解得![]() .
.
∴![]() (天).
(天).
答:日销售利润不超过1950元的共有18天.
(3)①当![]() 时,
时,![]() ,∴当
,∴当![]() 时,
时,![]() .
.
②当![]() 时,
时,![]() ,∴当
,∴当![]() 时,
时,![]() .
.
综上所述:当![]() 时,
时,![]() .
.
即第5日的销售利润最大,最大销售利润为1650元.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】为了迎接![]() 年高中招生考试,简阳市某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
年高中招生考试,简阳市某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给出的信息,解答下列问题:
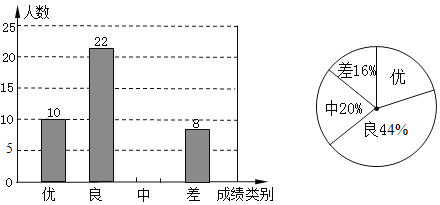
(1)在这次调查中,被抽取的学生的总人数为多少?
(2)请将表示成绩类别为“中”的条形统计图补充完整:
(3)在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是__________________:
(4)学校九年级共有![]() 人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.
(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为 3cm,求![]() 的长度.(结果保留π)
的长度.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
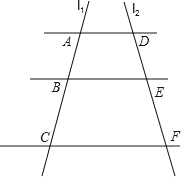
【题目】如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若![]() ,AC=14,
,AC=14,
(1)求AB的长.
(2)如果AD=7,CF=14,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+xy+2y-![]() ,B=2x2-2xy+x-1.
,B=2x2-2xy+x-1.
(1)求2A-B;
(2)当x=-1,y=-2时,求2A-B的值;
(3)若2A-B的值与x的取值无关,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
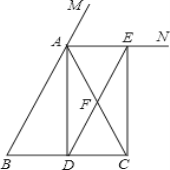
(1)求证:四边形ABDE是平行四边形;
(2)问:线段CE与线段AD有什么关系?请说明你的理由;
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了三束气球(每束![]() 个气球),每束价格如图所示,
个气球),每束价格如图所示,
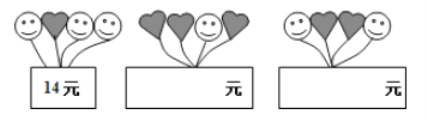
![]() 若笑脸气球的单价是
若笑脸气球的单价是![]() 元,请用含
元,请用含![]() 的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
![]() 若第②束气球的总价钱比第③束气球的总价钱少
若第②束气球的总价钱比第③束气球的总价钱少![]() 元,求这两种气球的单价.
元,求这两种气球的单价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com