
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
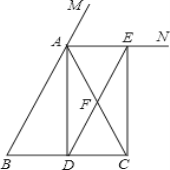
(1)求证:四边形ABDE是平行四边形;
(2)问:线段CE与线段AD有什么关系?请说明你的理由;
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?请说明你的理由.
【答案】(1)证明见解析;(2)CE∥AD,CE=AD;(3)答案不唯一,如∠BAC=90°.
【解析】
(1)由等腰三角形的性质和中位线的性质可证明:AB∥DE,再利用等腰三角形的性质和角平分线的定义证明AE∥BD,进而证明四边形ABDE的形状为平行四边形;
(2)CE∥AD,CE=AD;证明四边形ADCE为平行四边形即可;
(3)能使得矩形的邻边AD和DC相等的条件均可.
(1)四边形ABDE是平行四边形,理由如下:
∵AB=AC,D是BC中点,F是AC中点,
∴DF∥AB.
∵AB=AC,D是BC中点,
∴∠BAD=∠CAD,AD⊥DC.
∵AN是△ABC的外角∠MAC的角平分线,
∴∠MAE=∠CAE,∴∠NAD=90°,
∴AE∥BD,
∴四边形ABDE是平行四边形;
(2)CE∥AD,CE=AD.理由如下:
由(1)得:AE∥DC,AE=BD.
∵AB=AC,点D为BC中点,
∴BD=DC,
∴AE=DC.
∵AE∥DC,
∴四边形ADCE为平行四边形(有一组对边平行且相等的四边形是平行四边形),
∴CE∥AD,CE=AD.
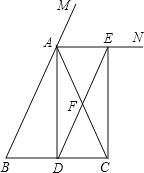
(3)答案不唯一,如当∠BAC=90°时,四边形ADCE是正方形.理由如下:
由(1)得:AD⊥BC,
∴∠ADC=90°.
∵四边形ADCE为平行四边形,
∴四边形ADCE为矩形.
∵∠BAC=90°,AB=AC,
∴△ABC为等腰直角三角形.
∵D为BC的中点,
∴AD=BD=DC,
∴矩形ADCE为正方形.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F.
(1)求证:四边形BEDF是平行四边形;
(2)当∠ABE为多少度时,四边形BEDF是菱形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发出一款新的节能产品,该产品的成本价为8元/件,该产品在正式投放市场前通过代销点进行了为期一个月30天的试销售,售价为13元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成如图所示的图象,图中的折线![]() 表示日销量
表示日销量![]() (件)与销售时间
(件)与销售时间![]() (天)之间的函数关系.
(天)之间的函数关系.
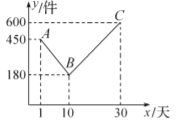
(1)直接写出![]() 与
与![]() 之间的函数解析式,并写出
之间的函数解析式,并写出![]() 的取值范围.
的取值范围.
(2)若该节能产品的日销售利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数解析式.日销售利润不超过1950元的共有多少天?
之间的函数解析式.日销售利润不超过1950元的共有多少天?
(3)若![]() ,求第几天的日销售利润最大,最大的日销售利润是多少元?
,求第几天的日销售利润最大,最大的日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最小的正整数,且
是最小的正整数,且![]() 、
、![]() 满足
满足![]() ,请回答问题:
,请回答问题:
(1)请直接写出![]() 、
、![]() 、
、![]() 的值.
的值.![]() ,
,![]() ,
,![]() .
.
(2)![]() 、
、![]() 、
、![]() 所对应的点分别为
所对应的点分别为![]() 、
、![]() 、
、![]() ,点
,点![]() 为一动点,其对应的数为
为一动点,其对应的数为![]() ,点
,点![]() 在
在![]() 、
、![]() 之间运动时,请化简式子:
之间运动时,请化简式子:![]() (请写出化简过程)
(请写出化简过程)
![]()
(3)在(1)(2)的条件下,点![]() 、
、![]() 、
、![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设经过
个单位长度的速度向右运动,假设经过![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .请问:
.请问:![]() 的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
的值是否随着时间的变化而改变?若变化,请说明理由:若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
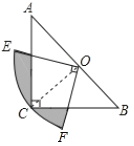
查看答案和解析>>
科目:初中数学 来源: 题型:
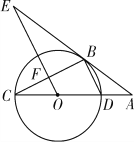
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是___(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,∠A=36°,AB的垂直平分线MD交AC于点D,AB于M,以下结论:①△BCD是等腰三角形;②射线BD是△ACB的角平分线;③△BCD的周长C△BCD=AC+BC;④△ADM≌BCD.正确的有( )
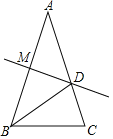
A.①②③B.①②C.①③D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com