
【题目】甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示。下列说法:①乙先到达青少年宫;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是___(填序号).

【答案】①②③.
【解析】
根据甲步行720米,需要9分钟,进而得出甲的运动速度,利用图形得出乙的运动时间以及运动距离,进而分别判断得出答案.
由图象得出甲步行720米,需要9分钟,
所以甲的运动速度为:720÷9=80(m/分),
当第15分钟时,乙运动159=6(分钟),
运动距离为:15×80=1200(m),
∴乙的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明乙已经到达终点,则乙先到达青少年宫,(故①正确);
此时乙运动199=10(分钟),
运动总距离为:10×200=2000(m),
∴甲运动时间为:2000÷80=25(分钟),
故a的值为25,(故④错误);
∵甲19分钟运动距离为:19×80=1520(m),
∴b=20001520=480,(故③正确).
故正确的有:①②③.
故答案为:①②③.


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,D是BC中点,F是AC中点,AN是△ABC的外角∠MAC的角平分线,延长DF交AN于点E.
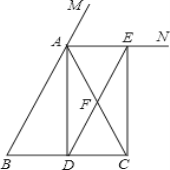
(1)求证:四边形ABDE是平行四边形;
(2)问:线段CE与线段AD有什么关系?请说明你的理由;
(3)当△ABC满足什么条件时,四边形ADCE是一个正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图如果以正方形![]() 的对角线
的对角线![]() 为边作第二个正方形
为边作第二个正方形![]() ,再以对角线
,再以对角线![]() 为边作第三个正方形
为边作第三个正方形![]() ,如此下去,…,已知正方形
,如此下去,…,已知正方形![]() 的面积
的面积![]() 为1,按上述方法所作的正方形的面积依次为
为1,按上述方法所作的正方形的面积依次为![]() ,
,![]() …
…![]() (
(![]() 为正整数),那么第8个正方形的面积
为正整数),那么第8个正方形的面积![]() __.
__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
⑴ 随机转动转盘一次,停止后(若指针落在分割线上,则重新转动,直至指向数字),指针指向数字1的概率是多少?(直接写出结果)
⑵ 小丽和小芳利用此转盘做游戏,游戏规则如下:自由转动转盘两次(若指针落在分割线上,则重转,直至指向数字),如果指针两次所指的数字之和为偶数,则小丽胜;否则,小芳胜.你认为对双方公平吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚 ,为了解揭阳市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷内容包括五个项目:
A:健身房运动;B:跳广场舞;C:参加暴走团;D:散步;E:不运动.
以下是根据调查结果绘制的统计图表的一部分,
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息,回答下列问题:
![]() 接受问卷调查的共有 人,图表中的
接受问卷调查的共有 人,图表中的![]() ,
,![]() .
.
![]() 统计图中,
统计图中,![]() 类所对应的扇形的圆心角的度数是 度.
类所对应的扇形的圆心角的度数是 度.

![]() 揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有
揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有![]() 人,请你估计一下该社区参加环岛路“暴走团”的人数.
人,请你估计一下该社区参加环岛路“暴走团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了三束气球(每束![]() 个气球),每束价格如图所示,
个气球),每束价格如图所示,
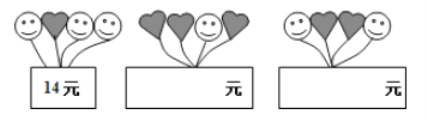
![]() 若笑脸气球的单价是
若笑脸气球的单价是![]() 元,请用含
元,请用含![]() 的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
的整式表示第②束、第③束气球的总价格; (要求结果化简后,填在方框内的相应位置上)
![]() 若第②束气球的总价钱比第③束气球的总价钱少
若第②束气球的总价钱比第③束气球的总价钱少![]() 元,求这两种气球的单价.
元,求这两种气球的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
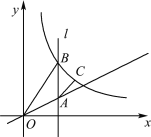
【题目】如图,已知点A是一次函数y=![]() x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=
x(x≥0)图象上一点,过点A作x轴的垂线l,B是l上一点(B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=![]() (x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
(x>0)的图象过点B,C,若△OAB的面积为5,则△ABC的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数![]() 的图象与性质
的图象与性质
(1)函数![]() 的自变量x的取值范围是___;
的自变量x的取值范围是___;
(2)下列四个函数图象中,函数![]() 的图象大致是___;
的图象大致是___;
A.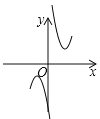 B.
B.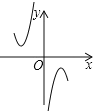 C.
C.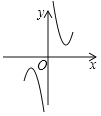 D.
D.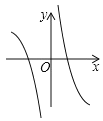
(3)对于函数![]() ,求当
,求当![]() 时,y的取值范围。
时,y的取值范围。
请将下面求解此问题的过程补充完整:
解:∵x>0
∴![]()
=![]()
∵![]()
∴y=____.
(拓展应用)
(4)若函数![]() ,求y的取值范围.
,求y的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com