
分析 (1)根据“和谐数”写出四个四位数的“和谐数”;设任意四位数“和谐数”形式为:abba(a、b为自然数),则这个四位数为a×103+b×102+b×10+a=1001a+110b,利用整数的整除得到$\frac{1001a+110b}{11}$=91a+10b,由此可判断任意四位数“和谐数”都可以被11整除;
(2)设能被11整除的三位“和谐数”为:xyx,则这个三位数为x•102+y•10+x=101x+10y,由于$\frac{101x+10y}{11}$=9x+y+$\frac{2x-y}{11}$,根据整数的整除性得到2x-y=0,于是可得y与x的关系式.
解答 解:(1)四位“和谐数”:1221,1331,1111,6666;
任意一个四位“和谐数”都能被11整数,理由如下:
设任意四位数“和谐数”形式为:abba(a、b为自然数),则a×103+b×102+b×10+a=1001a+110b,
∵$\frac{1001a+110b}{11}$=91a+10b
∴四位数“和谐数”abba能被11整数;
∴任意四位数“和谐数”都可以被11整除
(2)设能被11整除的三位“和谐数”为:xyx,则x•102+y•10+x=101x+10y,
$\frac{101x+10y}{11}$=9x+y+$\frac{2x-y}{11}$,
∵1≤x≤4,101x+10y能被11整除,
∴2x-y=0,
∴y=2x(1≤x≤4).
点评 本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.灵活利用整数的整除性.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
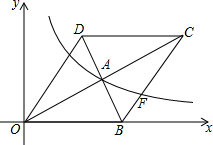 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是(12,$\frac{8}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
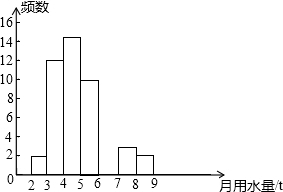 小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).| 月均用水量(单位:t) | 频数 | 百分比 |
| 2≤x<3 | 2 | 4% |
| 3≤x<4 | 12 | 24% |
| 4≤x<5 | 15 | 30% |
| 5≤x<6 | 10 | 20% |
| 6≤x<7 | 6 | 12% |
| 7≤x<8 | 3 | 6% |
| 8≤x<9 | 2 | 4% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )
如图,正比例函数y1=k1x的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,其中点A的横坐标为2,当y1>y2时,x的取值范围是( )| A. | x<-2或x>2 | B. | x<-2或0<x<2 | C. | -2<x<0或0<x<2 | D. | -2<x<0或x>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com