
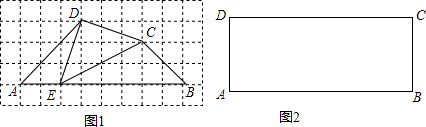
���� ��1��Ҫ֤����E���ı���ABCD��AB���ϵ����Ƶ㣬ֻҪ֤����һ�����������ƾ��У�������֤����ADE�ס�BEC����������ý⣻
��2������CDΪֱ��������ȡ�û���AB��һ�����㼴Ϊ��������DE��CE����AE=x����EB=8-x��AD=3�����ݵ�E���ı���ABCD��AB�ϵġ�ǿ���Ƶ㡱���õ���ADE�ס�BCE�����ǵõ�$\frac{AD}{BE}=\frac{AE}{BC}$�������������$\frac{3}{8-x}=\frac{x}{3}$���ⷽ�̼��ɵõ������
��� 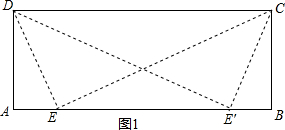 �⣺��1����ͼ��֪����A=��B=45�㣬
�⣺��1����ͼ��֪����A=��B=45�㣬
�ߡ�DEC=45�㣬
���AED+��ADE=135�㣬��AED+��CEB=135��
���ADE=��CEB��
���ADE�ס�BEC��
���E���ı���ABCD�ı�AB�ϵ����Ƶ㣮
��2������ͼ1��ʾ����AB���ϴ��ڵ�E��ʹ��EΪ�ı���ABCD��AB�ϵġ�ǿ���Ƶ㡱�������ĵ���2������E��E�伴Ϊ����
������DE��CE��
��AE=x��
��EB=8-x��AD=3��
�ߵ�E���ı���ABCD��AB�ϵġ�ǿ���Ƶ㡱��
���ADE�ס�BCE��
��$\frac{AD}{BE}=\frac{AE}{BC}$��
��AD=BC=3��
��$\frac{3}{8-x}=\frac{x}{3}$��
��ã�x=4��$\sqrt{7}$��
��AE=4+$\sqrt{7}$��AE=4-$\sqrt{7}$��
���� �����������������ۺ��⣬��Ҫ���������������εĶ�Ӧ�߳ɱ��������ʣ�������Ŀ��Ϣ������ǿ���Ƶ�Ķ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
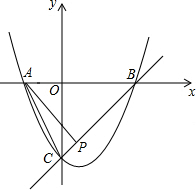 ��֪������y=x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C��O������ԭ�㣬��A�������ǣ�-1��0������C�������ǣ�0��-3����
��֪������y=x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C��O������ԭ�㣬��A�������ǣ�-1��0������C�������ǣ�0��-3�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
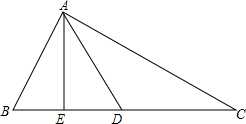 ��ͼ����֪��ABC�У�AD�����ߣ�AE�ǡ�ABD�����ߣ�BA=BD����BAD=��BDA����֤��AC=2AE��
��ͼ����֪��ABC�У�AD�����ߣ�AE�ǡ�ABD�����ߣ�BA=BD����BAD=��BDA����֤��AC=2AE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������Q/L | 60 | 50 | 40 | 30 | 20 | �� |
| ��ʻʱ��t/h | 0 | 2 | 4 | 6 | 8 | �� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com