
 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9.则下列结论错误的是( )
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9.则下列结论错误的是( )| A. | AE∥BC | B. | △ADE的周长是19 | ||
| C. | △BDE是等边三角形 | D. | ∠ADE=∠BDC |
分析 根据等边三角形的性质得∠ABC=∠C=60°,AC=BC=10,再根据旋转的性质得∠DBE=60°,BD=BE,AE=CD,∠EAB=∠C=60°,则∠EAB=∠ABC=60°,根据平行线的性质可对A选项进行判断;根据等边三角形的判定方法可对C选项进行判断;由于DE=BD=9,则可计算出△ADE的周长=DE+AC=19,于是可对B选项进行判断;先由△BDE是等边三角形得∠BDE=60°,再利用三角形外角性质可得∠ADE=∠DBC,然后根据三角形边角关系得∠BDC>∠DBC,所以∠BDC>∠ADE,于是可对D选项进行判断.
解答 解:∵△ABC为等边三角形,
∴∠ABC=∠C=60°,AC=BC=10,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠DBE=60°,BD=BE,AE=CD,∠EAB=∠C=60°,
∴∠EAB=∠ABC=60°,
∴AE∥BC;所以A选项的结论正确;
∵∠DBE=60°,BD=BE,
∴△BDE是等边三角形,所以C选项的结论正确;
∴DE=BD=9,
∴△ADE的周长=DE+AE+AD=DE+CD+AD=DE+AC=9+10=19,所以B选项的结论正确;
∵△BDE是等边三角形,
∴∠BDE=60°,
∵∠ADB=∠DBC+∠C,
∴∠ADE+60°=∠DBC+60°,
∴∠ADE=∠DBC,
∵BC>CD,
∴∠BDC>∠DBC,
∴∠BDC>∠ADE,所以D选项的结论错误.
故选D.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的判定与性质.


科目:初中数学 来源: 题型:选择题

| A. | 18-2a | B. | 18-4a | C. | 36-4a | D. | 36-8a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
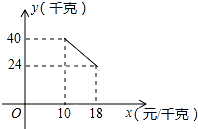 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5500(1+x)2=4000 | B. | 5500(1-x)2=4000 | C. | 4000(1-x)2=5500 | D. | 4000(1+x)2=5500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
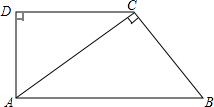 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
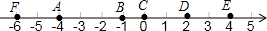 在如图所示的数轴上有A、B、C、D、E、F六个点,按要求完成下列各小题.
在如图所示的数轴上有A、B、C、D、E、F六个点,按要求完成下列各小题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com