
【题目】如图,AD∥BC,∠ABC=90°,AD=3,AB=4,点P为射线BC上一动点,以P为圆心,BP长为半径作⊙P,交射线BC于点Q,联结BD、AQ相交于点G,⊙P与线段BD、AQ分别相交于点E、F.
(1)如果BE=FQ,求⊙P的半径;
(2)设BP=x,FQ=y,求y关于x的函数关系式,并写出x的取值范围;
(3)联结PE、PF,如果四边形EGFP是梯形,求BE的长.

【答案】(1)⊙P的半径为![]() ;(2)x的取值范围为
;(2)x的取值范围为![]() ;(3)BE=
;(3)BE=![]() 或
或![]() .
.
【解析】
(1)由题意BE=FQ可得∠BPE=∠FPQ,进而可得∠EBP=∠FQP.又AD∥BC,故∠ADB=∠EBP,即∠FQP=∠ADB,故两角的正切值相等即可求出半径.
(2)要求y关于x的函数关系式即可通过过P点做垂线PM,将QM用含x的式子表示,利用QM=PQcos∠AQB=![]() ,而FQ=2QM,即
,而FQ=2QM,即![]() ;根据题意圆与D点相交时,x最大,可求出x的取值范围;
;根据题意圆与D点相交时,x最大,可求出x的取值范围;
(3)根据题意四边形EGFP是梯形,由于P点是动点所以产生两种情况,当GF∥EP时和GE∥FP时,故应进行分类讨论.①当GF∥EP时,可发现PE为△BGQ的中点,根据线段关系可求得BP的长度,因为△BGQ和△DGA相似,故有![]() ,可求得BG=
,可求得BG=![]() ,所以BE=
,所以BE=![]() BG.②当GE∥FP时,过点P作PN⊥BG ,跟①同理,可求得BE=2BN.
BG.②当GE∥FP时,过点P作PN⊥BG ,跟①同理,可求得BE=2BN.
(1)∵BE=FQ,
∴∠BPE=∠FPQ,
∵PE=PB,
∴∠EBP=![]() (180°﹣∠EPB),
(180°﹣∠EPB),
同理∠FQP=![]() (180°﹣∠FPQ),
(180°﹣∠FPQ),
∴∠EBP=∠FQP,
∵AD∥BC,
∴∠ADB=∠EBP,
∴∠FQP=∠ADB,
∴tan∠FQP=tan∠ADB=![]() ,
,
设⊙P的半径为r,则tan∠FQP=![]() ,
,
∴![]() ,
,
解得:r=![]() ,
,
∴⊙P的半径为![]() ;
;
(2)过点P作PM⊥FQ,垂足为点M,如图1所示:
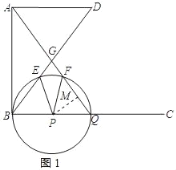
在Rt△ABQ中,cos∠AQB=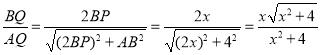 ,
,
在Rt△PQM中,QM=PQcos∠AQB=![]() ,
,
∵PM⊥FQ,PF=PQ,
∴FQ=2QM=![]() ,
,
∴![]() ,
,
当圆与D点相交时,x最大,作DH⊥BC于H,如图2所示:
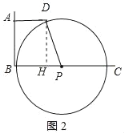
则PD=PB=x,DH=AB=4,BH=AD=3,
则PH=BP﹣BH=x﹣3,
在Rt△PDH中,由勾股定理得:42+(x﹣3)2=x2,
解得:x=![]() ,
,
∴x的取值范围为:0<x≤![]() ;
;
(3)设BP=x,分两种情况:
①EP∥AQ时,
∴∠BEP=∠BGQ,
∵PB=PE,
∴∠PBE=∠BEP,
∴∠BGQ=∠PBE,
∴QG=QB=2x,
同理:AG=AD=3,
在Rt△ABQ中,由勾股定理得:42+(2x)2=(3+2x)2,
解得:x=![]() ,
,
∴QG=QB=2x=![]() ,
,
∵EP∥AQ,PB=PQ,
∴BE=EG,
∵AD∥BC,
∴![]() ,
,
即 ,
,
解得:BG=![]() ,
,
∴BE=![]() BG=
BG=![]() ;
;
②PF∥BD时,同①得:BG=BQ=2x,DG=AD=3,
在Rt△ABD中,由勾股定理得:42+32=(3+2x)2,
解得:x=1或x=﹣4(舍去),
∴BQ=2,
∴BP=1,
作PN⊥BG于N,则BE=2BN,如图3所示:
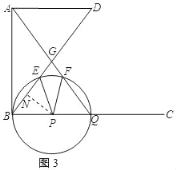
∵AD∥BC,
∴∠PBN=∠ADB,
∴cos∠PBN=cos∠ADB=![]() ,即
,即![]() =
=![]() ,
,
∴BN=![]() ,
,
∴BE=2BN=![]() ;
;
综上所述,BE=![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知:正方形![]() 中,
中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),易证
时(如图1),易证![]() .
.
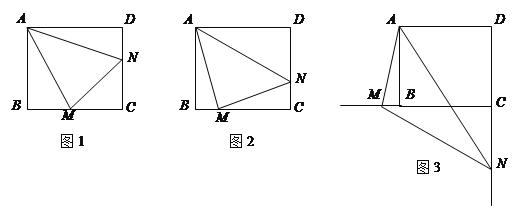
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),线段
时(如图2),线段![]() 和
和![]() 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.
(2)当![]() 绕点
绕点![]() 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段![]() 和
和![]() 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
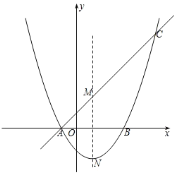
(1)求抛物线的函数关系式;
(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;
(3)在(2)的条件下,求△AQC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
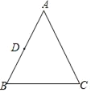
【题目】如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
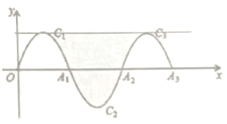
【题目】如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3,过抛物线C1,C3顶点的直线与C1、C2、C3围成的如图中的阴影部分,那么该面积为_____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是原点,
是原点,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() .
.

(1)以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 扩大为原来的两倍(即新图与原图的相似比为
扩大为原来的两倍(即新图与原图的相似比为![]() ),画出图形,并写出点
),画出图形,并写出点![]() 的对应点的坐标;
的对应点的坐标;
(2)如果![]() 内部一点
内部一点![]() 的坐标为
的坐标为![]() ,写出点
,写出点![]() 的对应点
的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,点A(0,6),点B在x轴的正半轴上.若点P,Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P,Q的“X矩形”.下图为点P,Q的“X矩形”的示意图.
(1)若点B(4,0),点C的横坐标为2,则点B,C的“X矩形”的面积为___.
(2)点M,N的“X矩形”是正方形,
①当此正方形面积为4,且点M到y轴的距离为3时,写出点B的坐标,点N的坐标.
②当此正方形的对角线长度为3,且半径为r的⊙O与它没有交点,直接写出r的取值范围___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x-3,下列说法中正确的是( )
A.该函数图象的开口向下B.该函数图象的顶点坐标是(-2,-7)
C.当x<0时,y随x的增大而增大D.该函数图象与x轴有两个不同的交点,且分布在坐标原点两侧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com