
已知,y=yl+y2,y1与x成正比例,y2与x成反比例,并且当x=﹣1时,y=﹣1,当x=2时,y=5.
(1)求y关于x的函数关系式;
(2)当y=﹣5时,求x的值.
【考点】待定系数法求反比例函数解析式.
【分析】(1)设y1=kx,y2=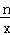 则y=y1+y2=kx+
则y=y1+y2=kx+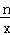 ,再把当x=﹣1时,y=﹣1,当x=2时,y=5代入可得
,再把当x=﹣1时,y=﹣1,当x=2时,y=5代入可得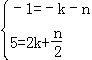 ,然后再解方程组即可得到k、n的值,进而可得答案;
,然后再解方程组即可得到k、n的值,进而可得答案;
(2)把y=﹣5代入(1)所得的函数解析式即可.
【解答】解:(1)设y1=kx,y2=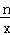 则y=y1+y2=kx+
则y=y1+y2=kx+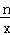 ,
,
∵当x=﹣1时,y=﹣1,当x=2时,y=5,
∴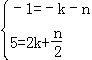 ,
,
解得: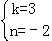 ,
,
∴y关于x的函数关系式为y=3x﹣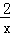 ;
;
(2)把y=﹣5代入y=3x﹣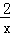 得:﹣5=3x﹣
得:﹣5=3x﹣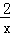 ,
,
解得:x1=﹣1,x2=﹣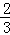 .
.
【点评】此题主要考查了待定系数法求反比例函数的解析式,关键是正确表示出函数解析式.


科目:初中数学 来源: 题型:
甲乙两队进行拔河比赛,标志物先向甲队方向移动0.5m,后向乙队方向移动了0.8m,相持一会后又向乙队方向移动0.5m,随后向甲队方向移动了1.5m在一片欢呼声中,标志物再向甲队方向移动1.2m.若规定只要标志物向某队方向移动2m,则该队即可获胜,那么现在甲队获胜了吗?用计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
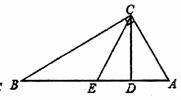
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线
的对称点E恰好为AB的中点,则∠B的度数是 ( )
A.30° B.45° C.60° D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
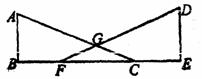
如图,点B、F、C、E存同一直线上, AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,.垂足为E,且AB=DE,BF=CE.
(1) 求证:△ABC≌△DEF;
(2) 若∠A=65°,求∠AGF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
a为有理数,定义运算符号“※”:当a>﹣2时,※a=﹣a,当a<﹣2时,※a=a,当a=﹣2时,※a=0,根据这种运算,则※[4+※(2﹣5)]的值为( )
A.1 B.﹣1 C.7 D.﹣7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com