
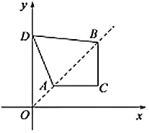
【题目】如图,在直角坐标系中,点![]() ,
,![]() 是第一象限角平分线上的两点,点
是第一象限角平分线上的两点,点![]() 的纵坐标为1,且
的纵坐标为1,且![]() ,在
,在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,使得四边形
,使得四边形![]() 的周长最小,这个最小周长的值为________.
的周长最小,这个最小周长的值为________.
【答案】![]()
【解析】
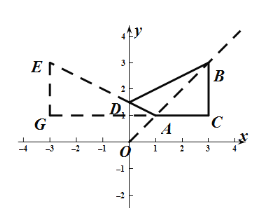
先求出AC=BC=2,作点B关于y轴对称的点E,连接AE,交y轴于D,此时AE=AD+BD,且AD+BD值最小,即此时四边形![]() 的周长最小;作FG∥y轴,AG∥x轴,交于点G,则GF⊥AG,根据勾股定理求出AE即可.
的周长最小;作FG∥y轴,AG∥x轴,交于点G,则GF⊥AG,根据勾股定理求出AE即可.
解:∵![]() ,点
,点![]() 的纵坐标为1,
的纵坐标为1,
∴AC∥x轴,
∵点![]() ,
,![]() 是第一象限角平分线上的两点,
是第一象限角平分线上的两点,
∴∠BAC=45°,
∵![]() ,
,
∴∠BAC=∠ABC=45°,
∴∠C=90°,
∴BC∥y轴,
∴AC=BC=2,
作点B关于y轴对称的点E,连接AE,交y轴于D,此时AE=AD+BD,且AD+BD值最小,
∴此时四边形![]() 的周长最小,
的周长最小,
作FG∥y轴,AG∥x轴,交于点G,则GF⊥AG,
∴EG=2,GA=4,
在Rt△AGE中,
![]() ,
,
∴ 四边形![]() 的周长最小值为2+2+
的周长最小值为2+2+![]() =4+
=4+![]() .
.


科目:初中数学 来源: 题型:
【题目】解答下列问题:
(1)阅读理解:
如图1,在![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.
的取值范围.
解决此问题可以用如下方法:延长![]() 到点
到点![]() 使
使![]() ,再连接
,再连接![]() (或将
(或将![]() 绕着
绕着![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() ,
,![]() 集中在
集中在![]() 中,利用三角形三边的关系即可判断.中线
中,利用三角形三边的关系即可判断.中线![]() 的取值范围是______.
的取值范围是______.

(2)问题解决:
如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() .
.
(3)问题拓展:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作一个
为顶点作一个![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,探索线段
,探索线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明.
之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育局为了了解线上教学对视力影响,对参加2020年中考的50000名初中毕业生回校后立即进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分.请根据图表信息回答下列问题:
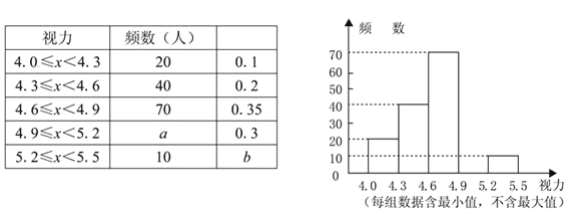
(1)在频数分布表中,a的值为________,b的值为________,并将频数分布直方图补充完整.
(2)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?
(3)若视力在4.9以上(含4.9)均属正常,求视力正常的人数占被统计人数的百分比,并根据上述信息估计全市初中毕业生中视力正常的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山地自行车越来越受年轻人的喜爱.某车行经营的A型山地自行车去年销售总额为30万元,今年每辆车售价比去年降低了200元.若卖出的数量相同,销售总额将比去年减少10%,
(1)今年A型车每辆售价多少元?
(2)该车行计划再进一批A型车和新款B型车共60辆,要使这批车获利不少于4万元,A型车至多进多少辆?
A、B两种型号车的进货和销售价格如表:
A型车 | B型车 | |
进货价格(元) | 1200 | 1400 |
销售价格(元) | 今年的销售价格 | 2200 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
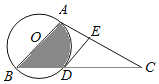
(1)求证:DE为⊙O的切线;
(2)若AB=4,∠ABC=30°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小吴家准备购买一台电视机,小吴将收集到的某地区A、B、C三种品牌电视机销售情况的有关数据统计如下:
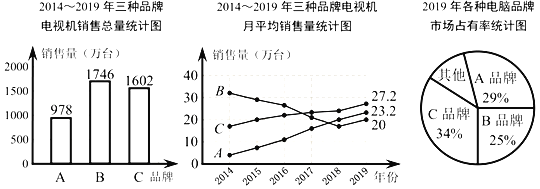
根据上述三个统计图,请解答:
(1)2014~2019年三种品牌电视机销售总量最多的是 品牌,月平均销售量最稳定的是 品牌.
(2)2019年其他品牌的电视机年销售总量是多少万台?
(3)货比三家后,你建议小吴家购买哪种品牌的电视机?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中
①三角形的外心到三角形的三个顶点的距离相等
②两条对角线相等的四边形是矩形
③将一次函数y=3x﹣1的图象不经过第四象限
④点A(x1,y1),B(x2,y2)都在反比例函数y=![]() 图象上,且x1<x2,则y1<y2
图象上,且x1<x2,则y1<y2
其中真命题有( )个
A.4个B.3个C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com