
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
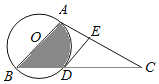
(1)求证:DE为⊙O的切线;
(2)若AB=4,∠ABC=30°,求阴影部分的面积.
【答案】(1)证明见解析;(2)![]() π+
π+![]() .
.
【解析】
(1)连接OD,如图,利用等腰三角形的性质和平行线的判定方法证明OD∥AC,则利用DE⊥AC得到OD⊥DE,然后根据切线的判定方法得到结论;
(2)过点O作OH⊥BD于H,如图,利用垂径定理得到BH=DH,再计算出∠AOD=60°,OH=1,BH=![]() ,然后利用扇形的面积公式,利用阴影部分的面积=S扇形AOD+S△OBD进行计算.
,然后利用扇形的面积公式,利用阴影部分的面积=S扇形AOD+S△OBD进行计算.
(1)证明:连接OD,如图,
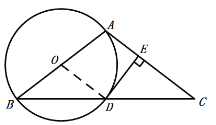
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)过点O作OH⊥BD于H,如图,则BH=DH,
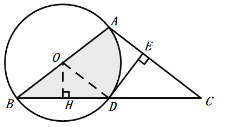
∵∠B=∠D=30°,
∴∠AOD=∠B+∠ODB=60°,OH=![]() OB=1,
OB=1,
∴BH=OH![]() =
=![]() ,
,
∴BD=2BH=2![]() ,
,
∴阴影部分的面积=S扇形AOD+S△OBD
=![]() ×2
×2![]() ×1
×1
=![]() π+
π+![]() .
.


科目:初中数学 来源: 题型:
【题目】金松科技生态农业养殖有限公司种植和销售一种绿色羊肚菌,已知该羊肚菌的成本是12元/千克,规定销售价格不低于成本,又不高于成本的两倍.经过市场调查发现,某天该羊肚菌的销售量y(千克)与销售价格x(元/千克)的函数关系如下图所示:
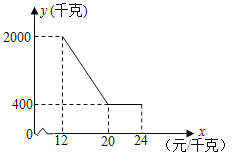
(1)求y与x之间的函数解析式;
(2)求这一天销售羊肚菌获得的利润W的最大值;
(3)若该公司按每销售一千克提取1元用于捐资助学,且保证每天的销售利润不低于3600元,问该羊肚菌销售价格该如何确定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y轴交于点N,其顶点为D.
(1)求抛物线及直线AC的函数关系式;
(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P的坐标;
(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
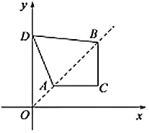
【题目】如图,在直角坐标系中,点![]() ,
,![]() 是第一象限角平分线上的两点,点
是第一象限角平分线上的两点,点![]() 的纵坐标为1,且
的纵坐标为1,且![]() ,在
,在![]() 轴上取一点
轴上取一点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() ,使得四边形
,使得四边形![]() 的周长最小,这个最小周长的值为________.
的周长最小,这个最小周长的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数![]() 在第二象限的图象经过点B,且
在第二象限的图象经过点B,且![]() ,则k的值 ( )
,则k的值 ( )
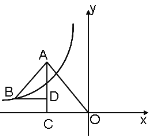
A.4B.8C.-4D.-8
查看答案和解析>>
科目:初中数学 来源: 题型:
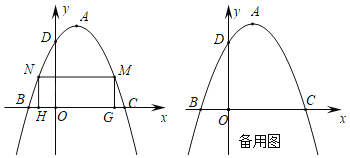
【题目】如图,已知二次函数图象的顶点坐标为A(1,4),与坐标轴交于B、C、D三点,且B点的坐标为(﹣1,0).
(1)求二次函数的解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3)当矩形MNHG的周长最大时,能否在二次函数图象上找到一点P,使△PNC的面积是矩形MNHG面积的![]() ?若存在,求出该点的横坐标;若不存在,请说明理由.
?若存在,求出该点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数![]() 图像,下列说法错误的是( )
图像,下列说法错误的是( )
A.其图象位于第一象限和第三象限
B.其图象上,在每一象限内,![]() 的值随
的值随![]() 的值的增大而减小
的值的增大而减小
C.其图象关于原点中心对称
D.![]() 为图象上任意一点,
为图象上任意一点,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,则矩形
,则矩形![]() 的面积为
的面积为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
调查结果扇形统计图
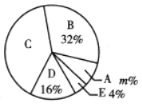
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ________,
________,![]() ________;
________;
(2)求扇形统计图中扇形![]() 的圆心角度数;
的圆心角度数;
(3)该校共有![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围的人数.
范围的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com