
【题目】已知![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 上一点(不与
上一点(不与![]() 重合),点
重合),点![]() 为射线
为射线![]() 上一点,
上一点,![]() ,设
,设![]() ,
,![]() .
.
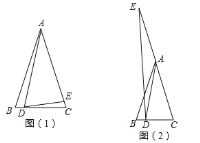
(1)如图1,①若![]() ,
,![]() ,则
,则![]() __________,
__________,![]() ___________.
___________.
②若![]() ,
,![]() ,则
,则![]() __________,
__________,![]() ___________.
___________.
③写出![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)如图2,当![]() 点在
点在![]() 的延长线上时,其它条件不变,请直接写出
的延长线上时,其它条件不变,请直接写出![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)①10°,5°;②16°,8°;③α=2β,理由见解析;(2)2β=180°+α,理由见解析
【解析】
(1)①直接求α度数,根据三角形的内角和与等腰三角形的性质求∠ACB和∠AED的度数再根据外角定理求β;②解法同①;③设∠BAC=x°,∠DAE=y°,则α=x°-y°,求出∠ACB和∠AED,利用外角定理即可求β,从而可得结论;
(2)设∠BAC=x°,∠DAE=y°,则α=x°-(180°-y°)=x°-180°+y°,同理得出出∠ACB和∠AED,利用外角定理即可求β,从而可得结论.
解:(1)①∵∠DAE=40°
∴∠ADE+∠AED=140°
∴∠ADE=∠AED=70°
∵∠BAC=50°
∴![]()
∴![]()
∵∠ADC=∠B+∠α=∠ADE+∠β
∴65°+10°=70°+∠β
∴∠β=5°
故答案为10°,5°;
②∵∠DAE=42°
∴∠ADE+∠AED=138°
∴∠ADE=∠AED=69°
∵∠BAC=58°
∴![]()
∴![]()
∵∠ADC=∠B+∠α=∠ADE+∠β
∴61°+16°=69°+∠β
∴∠β=8°
故答案为16°,8°;
③α=2β,理由是:
如图(1),设∠BAC=x°,∠DAE=y°,则α=x°-y°,
∵∠ACB=∠ABC
∴![]()
∵∠ADE=∠AED
∴![]()
∴![]()
∴α=2β
(2)如图(2),2β=180°+α,理由是:
设∠BAC=x°,∠DAE=y°,则α=x°-(180°-y°)=x°-180°+y°
∵∠ACB=∠ABC
∴![]()
∵∠ADE=∠AED
∴![]()
∵∠EDB是△EDC的一个外角
∴∠EDB=∠AED+∠ACB
∴![]()
∴2β=x°+y°,即2β=180°+α


科目:初中数学 来源: 题型:
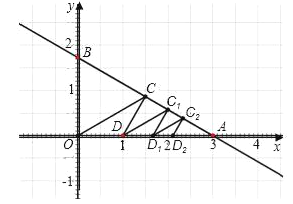
【题目】如图,在平面直角坐标系中,直线![]() 交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
交x轴于A点,交y轴于B点,点C是线段AB的中点,连接OC,然后将直线OC绕点C逆时针旋转30°交x轴于点D,再过D点作直线DC1∥OC,交AB与点C1,然后过C1点继续作直线D1C1∥DC,交x轴于点D1,并不断重复以上步骤,记△OCD的面积为S1,△DC1D1的面积为S2,依此类推,后面的三角形面积分别是S3,S4…,那么S1=_____,若S=S1+S2+S3+…+Sn,当n无限大时,S的值无限接近于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某市为处理污水,需要铺设一条长为4000米的管道,为了尽量减少施工对交通所造成的影响,实际施工时×××××.设原计划每天铺设管道x米,则可得方程![]() .”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
.”根据此情境,题中用“×××××”表示得缺失的条件,应补为( )
A.每天比原计划多铺设10米,结果延期20天才完成任务
B.每天比原计划少铺设10米,结果延期20天才完成任务
C.每天比原计划多铺设10米,结果提前20天完成任务
D.每天比原计划少铺设10米,结果提前20天完成任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
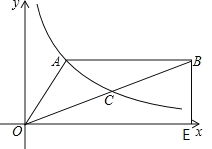
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,晚上小亮在广场上乘凉,图中线段AB表示站在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯.
请你再图中画出小亮在照明灯P照射下的影子BC;
如果灯杆高PO=12m,小亮的身高AB=1.6m,小亮与灯杆的距离BO=13m,请求出小亮影子的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
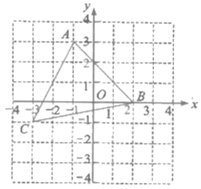
【题目】如图,在平面直角坐标系中有一个![]() ,顶点
,顶点![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于y轴的对称图形
关于y轴的对称图形![]() (不写画法);
(不写画法);
(2)点![]() 关于
关于![]() 轴对称的点的坐标为__________,点
轴对称的点的坐标为__________,点![]() 关于
关于![]() 轴对称的点的坐标为__________;
轴对称的点的坐标为__________;
(3)若网格上每个小正方形的边长为1,求![]() 的面积?
的面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com