
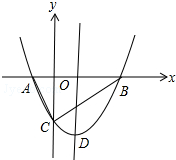
 如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 2 |
| 2 |


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图:
文明餐桌,拒绝“剩”宴!某中学发起“拒绝浪费,从我做起”的“光盘”行动!学校为了了解学生生活习惯是否符合“光盘”观念,在全校进行了一次问卷调查,若学生生活习惯符合“关盘”观念,则称其为“光盘族”;否则,称其为“非光盘族”.学校有七、八、九三个年级,经过统计,将全校的“光盘族”人数按年级绘制成如两幅统计图:查看答案和解析>>
科目:初中数学 来源: 题型:
| 原进价(元/个) | 零售价(元/个) | 成套售价(元/套) | |
| 螺丝 | 0.5 | 1.0 | 2.0 |
| 螺母 | 0.2 | 0.6 | 2.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com