
ЁОЬтФПЁПМзЁЂввСНИіХњЗЂЕъЯњЪлЭЌвЛжжЦЛЙћЃЌдкМзХњЗЂЕъЃЌВЛТлвЛДЮЙКТђЪ§СПЪЧЖрЩйЃЌМлИёОљЮЊ6дЊ/![]() ЃЎдкввХњЗЂЕъЃЌвЛДЮЙКТђЪ§СПВЛГЌЙ§
ЃЎдкввХњЗЂЕъЃЌвЛДЮЙКТђЪ§СПВЛГЌЙ§![]() ЪБЃЌМлИёЮЊ7дЊ/
ЪБЃЌМлИёЮЊ7дЊ/![]() ЃЛвЛДЮЙКТђЪ§СПГЌЙ§
ЃЛвЛДЮЙКТђЪ§СПГЌЙ§![]() ЪБЃЌЦфжага
ЪБЃЌЦфжага![]() ЕФМлИёШдЮЊ7дЊ/
ЕФМлИёШдЮЊ7дЊ/![]() ЃЌГЌЙ§
ЃЌГЌЙ§![]() ВПЗжЕФМлИёЮЊ5дЊ/
ВПЗжЕФМлИёЮЊ5дЊ/![]() ЃЎЩшаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ
ЃЎЩшаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉИљОнЬтвтЬюПеЃК
ЂйШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЂкШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЌдкввХњЗЂЕъЕФЛЈЗбЮЊ________дЊЃЛ
ЃЈЂђЃЉЩшдкМзХњЗЂЕъЛЈЗб![]() дЊЃЌдкввХњЗЂЕъЛЈЗб
дЊЃЌдкввХњЗЂЕъЛЈЗб![]() дЊЃЌЗжБ№Чѓ
дЊЃЌЗжБ№Чѓ![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈЂѓЃЉИљОнЬтвтЬюПеЃК
ЂйШєаЁЭѕдкМзХњЗЂЕъКЭдкввХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЯрЭЌЃЌЧвЛЈЗбЯрЭЌЃЌдђЫћдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ_________![]() ЃЛ
ЃЛ
ЂкШєаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЕФЪ§СПЮЊ![]() ЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ________ХњЗЂЕъЙКТђЛЈЗбЩйЃЛ
ЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ________ХњЗЂЕъЙКТђЛЈЗбЩйЃЛ
ЂлШєаЁЭѕдкЭЌвЛИіХњЗЂЕъвЛДЮЙКТђЦЛЙћЛЈЗбСЫ260дЊЃЌдђЫћдкМзЁЂввСНИіХњЗЂЕъжаЕФ_________ХњЗЂЕъЙКТђЪ§СПЖрЃЎ
ЁОД№АИЁПЃЈЂёЃЉЂй60ЃЌ70ЃЛЂк300ЃЌ290ЃЛЃЈЂђЃЉ![]() ЃЌ
ЃЌ![]() ЃЛЃЈЂѓЃЉЂй40ЃЛЂкМзЃЛЂлввЃЎ
ЃЛЃЈЂѓЃЉЂй40ЃЛЂкМзЃЛЂлввЃЎ
ЁОНтЮіЁП
ЃЈЂёЃЉЂйЗжБ№ИљОнзмМл=ЕЅМлЁСжиСПМДПЩМЦЫуЃЛ
ЂкМзХњЗЂЕъжБНгИљОнзмМл=ЕЅМлЁСжиСПМДПЩМЦЫуЃЌввХњЗЂЕъЕФЧА20kgАД7дЊМЦЫуЃЌКѓ30kgАД5дЊМЦЫуЃЌдйЯрМгМДПЩЃЛ
ЃЈЂђЃЉМзХњЗЂЕъжБНгИљОнзмМл=ЕЅМлЁСжиСПМДПЩМЦЫуЃЌввХњЗЂЕъашЖдxНјааЗжЖЮСаКЏЪ§НтЮіЪНЃЌЗжЮЊ0ЃМxЁм20КЭxЃО20СНжжЧщПіМДПЩНтД№ЃЛ
ЃЈЂѓЃЉЂйИљОнЛЈЗбЯрЭЌЃЌЕУГіxЃО20ЃЌдйСаГіЗНГЬМДПЩЯрЕШЃЛ
ЂкНЋx=30ЗжБ№ДњШы![]() ЃЌ
ЃЌ![]() жаМДПЩНтД№ЃЛ
жаМДПЩНтД№ЃЛ
ЂлЗжБ№НЋy=260ДњШы![]() ЃЌ
ЃЌ![]() МДПЩНтД№ЃЎ
МДПЩНтД№ЃЎ
НтЃКЃЈЂёЃЉЂйШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊЃК6ЁС10=60ЃЈдЊЃЉЃЌ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊЃК6ЁС10=60ЃЈдЊЃЉЃЌ
дкввХњЗЂЕъЕФЛЈЗбЮЊЃК7ЁС10=70ЃЈдЊЃЉ
ЙЪД№АИЮЊЃК60ЃЌ70ЃЛ
ЂкШєвЛДЮЙКТђЪ§СПЮЊ![]() ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊЃК6ЁС50=300ЃЈдЊЃЉЃЌ
ЪБЃЌдкМзХњЗЂЕъЕФЛЈЗбЮЊЃК6ЁС50=300ЃЈдЊЃЉЃЌ
дкввХњЗЂЕъЕФЛЈЗбЮЊЃК7ЁС20+5ЁСЃЈ50-20ЃЉ=290ЃЈдЊЃЉЃЌ
ЙЪД№АИЮЊЃК300ЃЌ290ЃЛ
ЃЈЂђЃЉдкМзХњЗЂЕъЛЈЗбЃК![]() ЃЌ
ЃЌ
ЕБ0ЃМxЁм20ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБxЃО20ЪБЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈЂѓЃЉЂйвђЮЊЕБ0ЃМxЁм20ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСНМвЕФЛЈЗбВЛПЩФмЯрЕШЃЌ
ЃЌСНМвЕФЛЈЗбВЛПЩФмЯрЕШЃЌ
ЁрxЃО20ЃЌ
дђ![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУx=40ЃЌ
ЃЌНтЕУx=40ЃЌ
ЙЪД№АИЮЊЃК40ЃЛ
ЂкЕБx=30ЪБЃЌ![]() ЃЈдЊЃЉЃЌ
ЃЈдЊЃЉЃЌ
![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
Ёп180ЃМ190ЃЌ
ЁрдкМзХњЗЂЕъЙКТђЛЈЗбЩйЃЌ
ЙЪД№АИЮЊЃКМзЃЛ
ЂлЕБy=260дЊЪБЃЌ
гЩ![]() ЃЌНтЕУЃКx=
ЃЌНтЕУЃКx=![]() ЃЈkgЃЉ
ЃЈkgЃЉ
ЁпЕБx=20ЪБЃЌ![]() ЃЌ
ЃЌ
ЁрxЃО20ЃЌ
гЩ![]() ЃЌНтЕУЃКx=44ЃЌ
ЃЌНтЕУЃКx=44ЃЌ
Ёп![]() ЃМ44ЃЌ
ЃМ44ЃЌ
ЁрдкввХњЗЂЕъЙКТђЕФЪ§СПЖрЃЌ
ЙЪД№АИЮЊЃКввЃЎ


 ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ
ШЪАЎгЂгяЭЌВНСЗЯАВсЯЕСаД№АИ бЇЯАЪЕМљдАЕиЯЕСаД№АИ
бЇЯАЪЕМљдАЕиЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
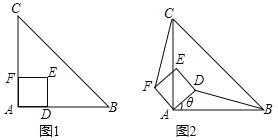
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯжЃКШчЭМ1ЃЌЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌЫФБпаЮADEFЪЧе§ЗНаЮЃЌЕуDЁЂFЗжБ№дкБпABЁЂACЩЯЃЌЧыжБНгаДГіЯпЖЮBDЁЂCFЕФЪ§СПКЭЮЛжУЙиЯЕЃЛ
ЃЈ2ЃЉЭиеЙЬНОПЃКШчЭМ2ЃЌЕБе§ЗНаЮADEFШЦЕуAФцЪБеыа§зЊШёНЧІШЪБЃЌЩЯЪіНсТлЛЙГЩСЂТ№ЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌНЋвЛОиаЮOABCЗХдкжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЕуAдкyжсе§АыжсЩЯЃЌЕуEЪЧБпABЩЯЕФвЛИіЖЏЕу![]() ВЛгыЕуAЁЂBжиКЯ
ВЛгыЕуAЁЂBжиКЯ![]() ЃЌЙ§ЕуEЕФЗДБШР§КЏЪ§
ЃЌЙ§ЕуEЕФЗДБШР§КЏЪ§![]() ЕФЭМЯѓгыБпBCНЛгкЕуF
ЕФЭМЯѓгыБпBCНЛгкЕуF
![]() Шє
Шє![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓkЕФжЕЃЛ
ЃЌЧѓkЕФжЕЃЛ
![]() Шє
Шє![]() ЃЌ
ЃЌ![]() ЃЌЗДБШР§КЏЪ§
ЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓгыБпABЁЂБпBCНЛгкЕуEКЭFЃЌЕБ
ЕФЭМЯѓгыБпABЁЂБпBCНЛгкЕуEКЭFЃЌЕБ![]() биEFелЕўЃЌЕуBЧЁКУТфдкOCЩЯЃЌЧѓkЕФжЕЃЎ
биEFелЕўЃЌЕуBЧЁКУТфдкOCЩЯЃЌЧѓkЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
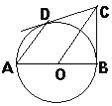
ЁОЬтФПЁПABЮЊЁбOжБОЖЃЌBCЮЊЁбOЧаЯпЃЌЧаЕуЮЊBЃЌCOЦНаагкЯвADЃЌзїжБЯпDCЃЎ
(1)ЧѓжЄЃКDCЮЊЁбOЧаЯпЃЛ
(2) ШєADЁЄOC=8ЃЌЧѓЁбOАыОЖЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкжБНЧШ§НЧаЮABCжаЃЌЁЯCЃН90ЁуЃЌACЃН2ЃЌBCЃН2![]() ЃЌЕуOЪЧБпABЩЯЕФвЛИіЖЏЕуЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖзїЁбOЃЌгыБпACНЛгкЕуMЃЎ
ЃЌЕуOЪЧБпABЩЯЕФвЛИіЖЏЕуЃЌвдЕуOЮЊдВаФЃЌOAЮЊАыОЖзїЁбOЃЌгыБпACНЛгкЕуMЃЎ
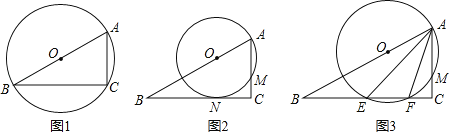
ЃЈ1ЃЉШчЭМ1ЃЌЕБЁбOОЙ§ЕуCЪБЃЌЁбOЕФжБОЖЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЁбOгыБпBCЯрЧаЪБЃЌЧаЕуЮЊЕуNЃЌЪдЧѓЁбOгыЁїABCжиКЯВПЗжЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБЁбOгыБпBCЯрНЛЪБЃЌНЛЕуЮЊEЁЂFЃЌЩшCMЃНxЃЌОЭХаЖЯAEAFЪЧЗёЮЊЖЈжЕЃЌШєЪЧЃЌЧѓГіетИіЖЈжЕЃЛШєВЛЪЧЃЌЧыгУКЌxЕФДњЪ§ЪНБэЪОЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
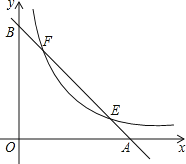
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпyЃНЉx+2ЗжБ№гыxжсЃЌyжсНЛгкAЃЌBСНЕуЃЌгыЫЋЧњЯпyЃН![]() НЛгкEЃЌFСНЕуЃЌШєABЃН2EFЃЌдђkЕФжЕЪЧ_____ЃЎ
НЛгкEЃЌFСНЕуЃЌШєABЃН2EFЃЌдђkЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
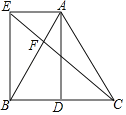
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌDЮЊBCжаЕуЃЌAEЁЮBDЃЌЧвAEЃНBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮAEBDЪЧОиаЮЃЛ
ЃЈ2ЃЉСЌНгCEНЛABгкЕуFЃЌШєЁЯABEЃН30ЁуЃЌAEЃН2ЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁзжМЦЛЎдкФГЭтТєЭјеОЕуШчЯТБэЫљЪОЕФВЫЦЗЃЌвбжЊУПЗнЖЉЕЅЕФХфЫЭЗбЮЊ3дЊЃЌЩЬМвЮЊСЫДйЯњЃЌЖдУПЗнЖЉЕЅЕФзмМлЃЈВЛКЌХфЫЭЗбЃЉЬсЙЉТњМѕгХЛнЃКТњ30дЊМѕ12дЊЃЌТњ60дЊМѕ30дЊЃЌТњ100дЊМѕ45дЊЃЌШчЙћаЁгюдкЙКТђЯТБэжаЫљгаВЫЦЗЪБЃЌВЩШЁЪЪЕБЕФЯТЖЉЕЅЗНЪНЃЌФЧУДЫћЕуВЭЕФзмЗбгУзюЕЭПЩЮЊ___дЊ.
ВЫЦЗ | ЕЅМлЃЈКЌАќзАЗбЃЉ | Ъ§СП |
| 30дЊ | 1 |
| 12дЊ | 1 |
| 30дЊ | 1 |
| 12дЊ | 1 |
| 3дЊ | 2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCгкЕуDЃЌЕуFЮЊABЩЯвЛЕуЃЌСЌНгCFЃЌЙ§ЕуBзїBEЁЭBCНЛCFЕФбгГЄЯпгкЕуEЃЌНЛADгкЕуHЃЌЧвЁЯ1=ЁЯ2
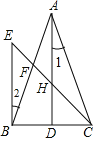
ЃЈ1ЃЉЧѓжЄЃКAB=ACЃЛ
ЃЈ2ЃЉШєЁЯ1=22ЁуЃЌЁЯAFC=110ЁуЃЌЧѓЁЯBCEЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com