
ЁОЬтФПЁПШчЭМ1ЃЌСНПщжБНЧШ§НЧжНАхЃЈRtЁїABCКЭRtЁїBDEЃЉАДШчЭМЫљЪОЕФЗНЪНАкЗХЃЈжиКЯЕуЮЊBЃЉЃЌЦфжаЁЯBDEЃНЁЯACBЃН90ЁуЃЌЁЯABCЃН30ЁуЃЌBDЃНDEЃНACЃН2ЃЎНЋЁїBDEШЦзХЕуBЫГЪБеыа§зЊЃЎ
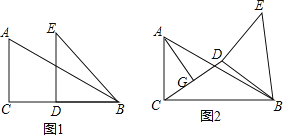
ЃЈ1ЃЉЕБЕуDдкBCЩЯЪБЃЌЧѓCDЕФГЄЃЛ
ЃЈ2ЃЉЕБЁїBDEа§зЊЕНAЃЌDЃЌEШ§ЕуЙВЯпЪБЃЌЛГіЯргІЕФВнЭМВЂЧѓЁїCDEЕФУцЛ§
ЃЈ3ЃЉШчЭМ2ЃЌСЌНгCDЃЌЕуGЪЧCDЕФжаЕуЃЌСЌНгAGЃЌЧѓAGЕФзюДѓжЕКЭзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2![]() Љ2ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉAGЕФзюаЁжЕЮЊ
Љ2ЃЛЃЈ2ЃЉ1ЃЛЃЈ3ЃЉAGЕФзюаЁжЕЮЊ![]() Љ1ЃЌAGЕФзюДѓжЕЮЊ
Љ1ЃЌAGЕФзюДѓжЕЮЊ![]() +1
+1
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌИљОнCDЃНBCЉBDЃЌжЛвЊЧѓГіBCМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЗжСНжжЧщаЮЗжБ№ЧѓНтЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМ4жаЃЌШЁBCЕФжаЕуHЃЌСЌНгGHЃЎгЩCGЃНGDЃЌCHЃНHBЃЌЭЦГіHGЃН![]() BDЃН1ЃЌПЩЕУЕуGЕФдЫЖЏЙьМЃЪЧвдHЮЊдВаФ1ЮЊАыОЖЕФдВЃЌИљОнЕугыдВЕФЮЛжУЙиЯЕМДПЩНтОіЮЪЬтЃЛ
BDЃН1ЃЌПЩЕУЕуGЕФдЫЖЏЙьМЃЪЧвдHЮЊдВаФ1ЮЊАыОЖЕФдВЃЌИљОнЕугыдВЕФЮЛжУЙиЯЕМДПЩНтОіЮЪЬтЃЛ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌ

дкRtЁїABCжаЃЌЁпЁЯCЃН90ЁуЃЌACЃН2ЃЌЁЯABCЃН30ЁуЃЌ
ЁрBCЃНACЁТtan30ЁуЃН2![]() ЃЌ
ЃЌ
ЁпBDЃН2ЃЌ
ЁрCDЃНBCЉBDЃН2![]() Љ2ЃЎ
Љ2ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌЕБAЁЂDЁЂEЙВЯпЪБЃЌвзжЄЫФБпаЮACBDЪЧОиаЮЃЌ

ЁрSЁїCDEЃН![]() ЁСDEЁСCAЃН
ЁСDEЁСCAЃН![]() ЁС2ЁС2ЃН2ЃЎ
ЁС2ЁС2ЃН2ЃЎ
ШчЭМ3жаЃЌЕБAЁЂEЁЂDЙВЯпЪБЃЌзїCHЁЭADгкHЃЎ
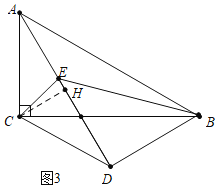
дкRtЁїADBжаЃЌЁпABЃН2BDЃЌ
ЁрЁЯBADЃН30ЁуЃЌ
ЁпЁЯCABЃН60ЁуЃЌ
ЁрЁЯCAHЃН30ЁуЃЌ
ЁрCHЃН![]() ACЃН1ЃЌ
ACЃН1ЃЌ
ЁрSЁїCDEЃН![]() ЁСDEЁСCHЃН
ЁСDEЁСCHЃН![]() ЁС2ЁС1ЃН1ЃЎ
ЁС2ЁС1ЃН1ЃЎ
ЃЈ3ЃЉШчЭМ4жаЃЌШЁBCЕФжаЕуHЃЌСЌНгGHЃЎ
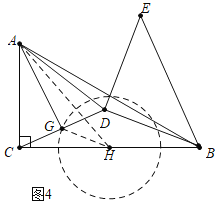
ЁпCGЃНGDЃЌCHЃНHBЃЌ
ЁрHGЃН![]() BDЃН1ЃЌ
BDЃН1ЃЌ
ЁрЕуGЕФдЫЖЏЙьМЃЪЧвдHЮЊдВаФ1ЮЊАыОЖЕФдВЃЌ
дкRtЁїACHжаЃЌAHЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрAGЕФзюаЁжЕЃНAHЉGHЃН![]() Љ1ЃЌ
Љ1ЃЌ
AGЕФзюДѓжЕЃНAH+GHЃН![]() +1
+1



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкВЛЭИУїЕФВМДќжазАга1ИіКьЧђЃЌ2ИіАзЧђЃЌЫќУЧГ§беЩЋЭтЦфгрЭъШЋЯрЭЌЃЎ
ЃЈ1ЃЉДгДќжаШЮвтУўГіСНИіЧђЃЌЪдгУЪїзДЭМЛђБэИёСаГіЫљгаЕШПЩФмЕФНсЙћЃЌВЂЧѓУўГіЕФЧђЧЁКУЪЧСНИіАзЧђЕФИХТЪЃЛ
ЃЈ2ЃЉШєдкВМДќжадйЬэМгaИіАзЧђЃЌГфЗжНСдШЃЌДгжаУўГівЛИіЧђЃЌЪЙУўЕНКьЧђЕФИХТЪЮЊ![]() ЃЌЪдЧѓaЕФжЕЃЎ
ЃЌЪдЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=Љx2+2mxЉm2+1ЕФЖдГЦжсЪЧжБЯпx=1ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуDЃЈnЃЌy1ЃЉЃЌEЃЈ3ЃЌy2ЃЉдкХзЮяЯпЩЯЃЌШєy1ЃМy2ЃЌЧыжБНгаДГіnЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшЕуMЃЈpЃЌqЃЉЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЉ1ЃМpЃМ2ЪБЃЌЕуMЙигкyжсЕФЖдГЦЕуЖМдкжБЯпy=kxЉ4ЕФЩЯЗНЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌНЋОиаЮ
ЃЌНЋОиаЮ![]() бижБЯп
бижБЯп![]() ЗелЃЌЕу
ЗелЃЌЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ДІЃЌдђ
ДІЃЌдђ![]() __________ЃЎ
__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮЭјИёжаЃЌ![]() ЕФЖЅЕуОљдкИёЕуЩЯЃЌЧыдкЫљИјжБНЧзјБъЯЕжаАДвЊЧѓЛЭМКЭНтД№ЯТСаЮЪЬтЃК
ЕФЖЅЕуОљдкИёЕуЩЯЃЌЧыдкЫљИјжБНЧзјБъЯЕжаАДвЊЧѓЛЭМКЭНтД№ЯТСаЮЪЬтЃК
![]() вддЕу
вддЕу![]() ЮЊЖдГЦжааФЃЌЛГі
ЮЊЖдГЦжааФЃЌЛГі![]() ЕФжааФЖдГЦЭМаЮ
ЕФжааФЖдГЦЭМаЮ![]() ЃЎ
ЃЎ
![]() вддЕу
вддЕу![]() ЮЊЮЛЫЦжааФЃЌдкдЕуЕФСэвЛВрЛГі
ЮЊЮЛЫЦжааФЃЌдкдЕуЕФСэвЛВрЛГі![]() ЕФЮЛЫЦШ§НЧаЮ
ЕФЮЛЫЦШ§НЧаЮ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФЮЛЫЦБШЮЊ
ЕФЮЛЫЦБШЮЊ![]() ЃЛ
ЃЛ
![]() ЕФУцЛ§
ЕФУцЛ§![]() ________ЃЎ
________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
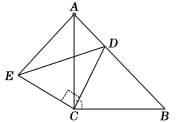
ЁОЬтФПЁПШчЭМЃЌЁїACBКЭЁїECDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=ЁЯECD=90ЁуЃЌDЮЊABБпЩЯвЛЕуЃЎ
ЧѓжЄЃКЃЈ1ЃЉЁїACEЁеЁїBCDЃЛЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊx2+ЃЈa+3ЃЉx+a+1ЃН0ЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬЃЎ
ЃЈ1ЃЉЧѓжЄЃКЗНГЬзмгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЛ
ЃЈ2ЃЉШєЗНГЬЕФвЛИіЪЕЪ§ИљЮЊ1ЃЌЧѓЪЕЪ§aЕФжЕКЭСэвЛИіЪЕЪ§ИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєвЛИіШ§НЧаЮвЛЬѕБпЕФЦНЗНЕШгкСэСНЬѕБпЕФГЫЛ§ЃЌЮвУЧАбетИіШ§НЧаЮНазіБШР§Ш§НЧаЮЃЎ

ЃЈ1ЃЉвбжЊЁїABCЪЧБШР§Ш§НЧаЮЃЌABЃН2ЃЌBCЃН3ЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФACЕФГЄЃЛ
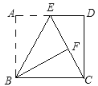
ЃЈ2ЃЉШчЭМ1ЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЖдНЧЯпBDЦНЗжЁЯABCЃЌЁЯBACЃНЁЯADCЃЎ
ЂйЧѓжЄЃКЁїABCЁзЁїDCAЃЛЂкЧѓжЄЃКЁїABCЪЧБШР§Ш§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБЁЯADCЃН90ЁуЪБЃЌЧѓГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌАыОЖЮЊ5ЕФЁбAжаЃЌЯвBCЃЌEDЫљЖдЕФдВаФНЧЗжЪЧЁЯBACЃЌЁЯEADЃЌШєDE=6ЃЌЁЯBAC+ЁЯEAD=180ЁуЃЌдђдВаФAЕНЯвBCЕФОрРыЕШгкЃЈЁЁЁЁЃЉ
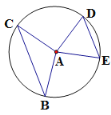
A.![]() B.
B.![]() C.4D.3
C.4D.3
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com