练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知x2+（a+3）x+a+1＝0是关于x的一元二次方程．

    （1）求证：方程总有两个不相等的实数根；

    （2）若方程的一个实数根为1，求实数a的值和另一个实数根．

    【答案】（1）见解析；（2）x＝1或x＝﹣．

    【解析】

    （1）求出判别式△=（a+1）2+4＞0，据此可得答案；

    （2）将x=1代入方程，求出a的值，据此得出方程，再利用因式分解法求解可得．

    （1）∵△＝（a+3）2﹣4（a+1）

    ＝a2+6a+9﹣4a﹣4

    ＝a2+2a+5

    ＝（a+1）2+4＞0，

    ∴方程总有两个不相等的实数根；

    （2）将x＝1代入方程，得：1+a+3+a+1＝0，

    解得a＝﹣，

    则方程为x2+x﹣＝0，

    ∴（x﹣1）（2x+3）＝0，

    则x﹣1＝0或2x+3＝0，

    解得x＝1或x＝﹣．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2＋(2k－1)x＋k2－1＝0有两个实数根x1，x2．

    (1)求实数k的取值范围；

    (2)若x1，x2满足x12＋x22＝16＋x1x2，求实数k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

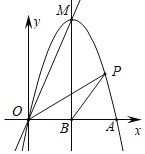
    【题目】如图，抛物线y＝ax2+bx（a≠0）交x轴正半轴于点A，直线y＝2x经过抛物线的顶点M．已知该抛物线的对称轴为直线x＝2，交x轴于点B．

    （1）求M点的坐标及a，b的值；

    （2）P是第一象限内抛物线上的一点，且在对称轴的右侧，连接OP，BP．设点P的横坐标为m，△OBP的面积为S，当m为多少时，s＝．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，两块直角三角纸板（Rt△ABC和Rt△BDE）按如图所示的方式摆放（重合点为B），其中∠BDE＝∠ACB＝90°，∠ABC＝30°，BD＝DE＝AC＝2．将△BDE绕着点B顺时针旋转．

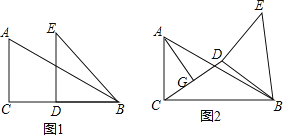
    （1）当点D在BC上时，求CD的长；

    （2）当△BDE旋转到A，D，E三点共线时，画出相应的草图并求△CDE的面积

    （3）如图2，连接CD，点G是CD的中点，连接AG，求AG的最大值和最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：

    ①2a+b=0；②abc＞0；③方程ax2+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，

    其中正确的是（ ）

    A. ①②③ B. ①③④ C. ①③⑤ D. ②④⑤

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知等边△ABC.
    (1)请用圆规和直尺作△ABC的内切圆(要求保留作图痕迹,不必写作法和证明)；
    (2)若等边△ABC边长为2，求△ABC的内切圆的半径.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解方程：

    （1）（2x﹣5）2﹣9＝0

    （2）4x2+2x﹣1＝0

    （3）（x﹣1）2+2x（x﹣1）＝0

    （4）x2+6x﹣9991＝0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：二次函数y=x2+bx+3的图象经过点(3，0).

    （1）求b的值；

    （2）求出该二次函数图象的顶点坐标和对称轴；

    （3）在所给坐标系中画出二次函数y=x2+bx+3的图象.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

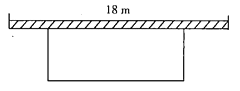
    【题目】如图，学校准备在教学楼后面搭建一简易矩形自行车车棚，一边利用教学楼的后墙（可利用的墙长为18m），另外三边利用学，校现有总长38m的铁栏围成．

    （1）若围成的面积为，试求出自行车车棚的长和宽；

    （2）能围成面积为的自行车车棚吗？如果能，请你给出设计方案；如果不能，请说明理由．

    查看答案和解析>>

    同步练习册答案