
B
【解析】连接EC,交AD于点P,次数EP+BP的值最小,过点E作EF⊥BC,则有BD=CD=2,由勾股定理,可
得AD=2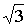 ,同时可得EF∥AD,△BEF∽△BAD,所以
,同时可得EF∥AD,△BEF∽△BAD,所以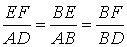 ,解得BF=1.5,FD=0.5,EF=
,解得BF=1.5,FD=0.5,EF= ,所以EC=
,所以EC=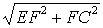 =
= ,所求的最小值是
,所求的最小值是 .
.
(1)AE∥BD,且AE=BD.(2)16;(3)当∠ACB=60°时,四边形ABFE为矩形.
【解析】(1)AE∥BD,且AE=BD.理由如下:∵将△ABC绕点C顺时针旋转180°得到△DEC,∴△ABC≌△DEC,∴AB=DE,∠ABC=∠DEC,∴AB∥DE,∴四边形ABDE是平行四边形,∴AE∥BD,且AE=BD;
(2)由(1)得四边形ABFE为平行四边形,∴AC=CF,BC=CE,∴根据等底同高得到S△ABC=S△ACE=S△BCF=S△CEF=4,S四边形ABFE=4S△ABC=16cm2;
(3)当∠ACB=60°时,四边形ABFE为矩形.
理由是:AB=AC,∠ACB=60°,∴△ABC是等边三角形,∴BC=AC,∠BAC=60°,∴∠ACE=120°.又BC=CE,AC=CF,∴∠EAC=∠CEA=30°,∴∠BAE=90°,同理可证其余三个角也为直角.∴四边形ABFE为矩形.


科目:初中数学 来源: 题型:
某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”,“科技制作”,“数学思维”,“阅读写作”这四个选修项目的学生(每人限报一课)进行抽样调查,下面是根据收集的数据绘制的不完整的统计图,请根据图中提供的信息,解答下面的问题:

(1)此次共调查了______名学生,扇形统计图中“艺术鉴赏”部分的圆心角是______度;
(2)请把这个条形统计图补充完整;
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
C.
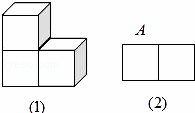
【解析】根据本题的题意,由主视图可设计该几何体 如图:想得到题意中的俯视图,只需在图(2)中的A位置添加一个或叠放1个或两个小正方形,故组成这个几何体的小正方形的个数为4个或5个.
如图:想得到题意中的俯视图,只需在图(2)中的A位置添加一个或叠放1个或两个小正方形,故组成这个几何体的小正方形的个数为4个或5个.
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有( ).
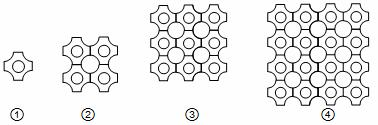
A.100个 B.101个 C.181个 D.221个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com