
如图①是一块瓷砖的图案,用这种瓷砖铺设地面,如果铺设成如图②的图案,其中完整的圆一共有5个,如果铺设成如图③的图案,其中完整的圆一共有13个,如果铺设成如图④的图案,其中完整的圆一共有25个,以此规律下去,第10个图中,完整的圆一共有( ).
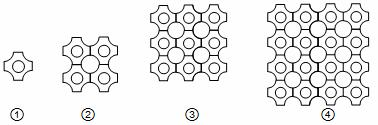
A.100个 B.101个 C.181个 D.221个
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
B
【解析】连接EC,交AD于点P,次数EP+BP的值最小,过点E作EF⊥BC,则有BD=CD=2,由勾股定理,可
得AD=2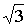 ,同时可得EF∥AD,△BEF∽△BAD,所以
,同时可得EF∥AD,△BEF∽△BAD,所以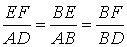 ,解得BF=1.5,FD=0.5,EF=
,解得BF=1.5,FD=0.5,EF= ,所以EC=
,所以EC=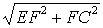 =
= ,所求的最小值是
,所求的最小值是 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形AOCD的顶点A的坐标是(0,4).动点P从点O出发沿线段OC(不包括端点O,C)以每秒2个单位长度的速度匀速向点C运动,同时动点Q从点C出发沿线段CD(不包括端点C,D)以每秒1个单位长度的速度匀速向点D运动.当其中一点到达终点时,另一点也停止运动.设运动时间为t(秒),当t=2(秒)时,PQ= .解答下列问题:
.解答下列问题:

(1)求点D的坐标;
(2)直接写出t的取值范围;
(3)连接AQ并延长交x轴于点E,把AQ沿AD翻折,点Q落在CD延长线上点F处,连接EF.
①t为何值时,PQ∥AF;
②△AEF的面积S是否随t的变化而变化?若变化,求出S与t的函数关系式;若不变化,求出S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,直线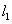 的解析表达式为
的解析表达式为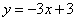 ,且
,且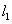 与
与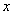 轴交于点D,直线
轴交于点D,直线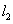 经过点A,B,直线
经过点A,B,直线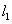 和
和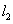 交于点C.
交于点C.
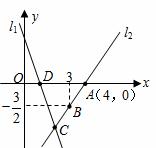
(1)求直线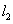 的解析表达式;
的解析表达式;
(2)求△ADC的面积;
(3)直线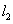 上存在异于点C的另一点P,使△ADP与△ADC面积相等,求出点P的坐标.
上存在异于点C的另一点P,使△ADP与△ADC面积相等,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com