
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证![]() ;
;
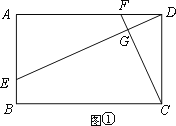
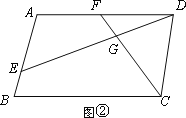
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
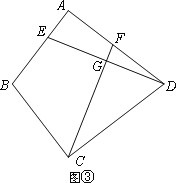
(3)如图③,若BA=BC=4,DA=DC=6,∠BAD=90°,DE⊥CF,请直接写出![]() 的值.
的值.
【答案】(1)(2)见解析;(3)![]()
【解析】分析:(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)当∠B+∠EGC=180°时,![]() 成立,证△DFG∽△DEA,得出
成立,证△DFG∽△DEA,得出![]() ,证△CGD∽△CDF,得出
,证△CGD∽△CDF,得出![]() ,即可得出答案;
,即可得出答案;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=![]() ,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-4)2+(
,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-4)2+(![]() )2=42,求出CN=
)2=42,求出CN=![]() ,证出△AED∽△NFC,即可得出答案.
,证出△AED∽△NFC,即可得出答案.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠ADC=90°.
∴∠ADE+∠CDE=90°.
∵DE⊥CF,∴∠DCF+∠CDE=90°.
∴∠ADE=∠DCF.
∴△ADE∽△DCF,∴![]() .
.
(2)当∠B+∠EGC=180°时,![]() 成立.
成立.
证明如下:在AD的延长线上取点M,使CM=CF,则∠CMF=∠CFM.
∵AB∥CD,AD∥BC,∴∠A=∠CDM. ,∠CFM=∠FCB.
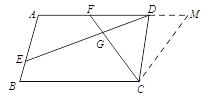
∵∠B+∠EGC=180°,∴∠FCB+∠BEG=180°.
∵∠AED+∠BEG=180°,∴∠AED=∠FCB.
∴∠CMF=∠AED.
∴△ADE∽△DCM.
∴![]() .即
.即![]() .
.
(3)![]() .
.
过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,

∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,
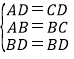
∴△BAD△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() ,
,
∴![]() ,
,
∴CM=![]() ,
,
在Rt△CMB中,CM=![]() ,BM=AM-AB=x-4,由勾股定理得:BM2+CM2=BC2,
,BM=AM-AB=x-4,由勾股定理得:BM2+CM2=BC2,
∴(x-4)2+(![]() )2=42,
)2=42,
x=0(舍去),x=![]() ,
,
CN=![]() ,
,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 的距离
的距离![]() 倍,我们就称点
倍,我们就称点![]() 是
是![]() 的巧点.若
的巧点.若 ![]() 为数轴上三点,若点
为数轴上三点,若点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到 ![]() 的距离一半,我们就称点
的距离一半,我们就称点![]() 是
是![]() 的妙点.如图,点
的妙点.如图,点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,表示
,表示![]() 的点
的点![]() 到点
到点![]() 的距离是
的距离是![]() ,到点
,到点![]() 的距离是
的距离是![]() ,那么点
,那么点![]() 是
是![]() 的巧点,点
的巧点,点![]() 是
是![]() 的妙点.
的妙点.
![]()
知识运用:
(1)如图 1,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,点
,点![]() 表示的数是
表示的数是![]() ,那么点
,那么点![]() 是(
是(![]() 的( )
的( )
![]()
A.巧点 B. 妙点 C. 无法确定
(2)如图 2,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() ,则(
,则(![]() 的巧点表示的数是 ;
的巧点表示的数是 ;
![]()

拓展提升
(3)如图 3,![]() 为数轴上两点,点
为数轴上两点,点![]() 所表示的数为
所表示的数为![]() ,点
,点![]() 所表示的数为
所表示的数为![]() .现有一只电子蚂蚁P从点
.现有一只电子蚂蚁P从点 ![]() 出发,以每
出发,以每![]() 秒单位的速度向右运动,到达点
秒单位的速度向右运动,到达点![]() 停止. 当经过几秒时,
停止. 当经过几秒时,![]() 和
和 ![]() 其有一个点为其余两点的巧点? (请直接写出结果)
其有一个点为其余两点的巧点? (请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长5m的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为4m,如果梯子的顶端A沿墙下滑1m至C点.
(1)求梯子底端B外移距离BD的长度;
(2)猜想CE与BE的大小关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
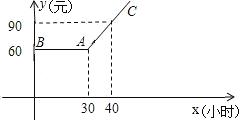
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
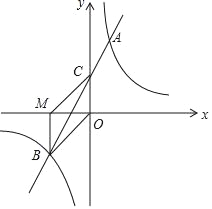
【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人各射击![]() 次,甲所中的环数是
次,甲所中的环数是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且甲所中的环数的平均数是
,且甲所中的环数的平均数是![]() ,众数是
,众数是![]() ;乙所中的环数的平均数是
;乙所中的环数的平均数是![]() ,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )
,方差是4.根据以上数据,对甲,乙射击成绩的正确判断是( )
A.甲射击成绩比乙稳定B.乙射击成绩比甲稳定
C.甲,乙射击成绩稳定性相同D.甲、乙射击成绩稳定性无法比较
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若a+b=2,则称a与b是关于1的平衡数.
(1)①3与 是关于1的平衡数;②4﹣x与 是关于1的平衡数(用含x的代数式表示).
(2)若a=2x2﹣3(x2+x)﹣4,b=2x﹣[3x﹣(4x+x2)﹣2],判断a与b是否是关于1的平衡数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校羽毛球队需要购买6支羽毛球拍和x盒羽毛球,羽毛球拍市场价为200元/支,羽毛球为30元/盒.甲商场优惠方案为:所有商品9折.乙商场优惠方案为:买1支羽毛球拍送1盒羽毛球,其余原价销售.
![]() 当
当![]() 大于
大于![]() 时,分别用含
时,分别用含![]() 的代数式表示在甲商场和乙商场购买所有物品的费用.
的代数式表示在甲商场和乙商场购买所有物品的费用.
![]() 当
当![]() 时,请你通过计算说明选择哪个商场购买比较省钱.
时,请你通过计算说明选择哪个商场购买比较省钱.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com