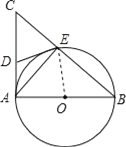
【题目】如图，AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E，连接AE．

（1）若D为AC的中点，连接DE，证明：DE是⊙O的切线；

（2）若BE=3EC，求tan∠ABC．

参考答案：

【答案】见解析

【解析】试题分析：（1）要证明DE是⊙O的切线，只要证明等于90°即可，由题可得 =90°，从题上条件可得, ,所以可以得出=90°，从而得出要求证结论。（2）BE=3EC，要想利用这个条件，可放在ECA和EAB中，证明ECAEAB，即可得到对应边成比例，进而得到AE、EC、EB三者之间的关系，再利用BE=3EC，求得tan∠ABC。

试题解析：证明：（1）连接OE，

∵AB是⊙O的直径，AC是圆⊙O的切线，

∴AE⊥BC，AC⊥AB，

在直角△AEC中，

∵D为AC的中点，

∴DE=DC，∴∠DEC=∠DCE，

∵∠OEB=∠OBE，∠ABC+∠ACB=90°，

∴∠DEC+∠OEB=∠DCE+∠OBE=90°，

∴∠DEO=180°﹣90°=90°，∴OE⊥DE，

∴DE 是⊙O的切线；

（2）在直角△EAC与直角△EBA中，

∵∠EAC+∠EAB=90°，∠EBA+∠EAB=90°，

∴∠EAC=∠EBA，

∴△EAC∽△EBA，

∴，EA2=EBEC

设EC=1，则EB=3，

EA2=EBEC=3， ，

在直角△AEB中， ．

关闭