
【题目】如图,将一个三角板![]() ,绕点
,绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,且
,且![]() ,
,![]() ,则线段
,则线段![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接![]() ,延长
,延长![]() 交
交![]() 于点
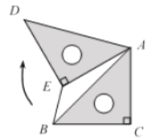
于点![]() ,根据旋转性质可知AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,由此得出△ABD为等边三角形,然后进一步通过证明△BAE△BDE得出∠ABE=∠DBE,根据等腰三角形“三线合一”可知BF⊥AD,且AF=DF,由此利用勾股定理分别计算出AB、BF的长,最后通过BE=BFEF进一步计算即可得出答案.
,根据旋转性质可知AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,由此得出△ABD为等边三角形,然后进一步通过证明△BAE△BDE得出∠ABE=∠DBE,根据等腰三角形“三线合一”可知BF⊥AD,且AF=DF,由此利用勾股定理分别计算出AB、BF的长,最后通过BE=BFEF进一步计算即可得出答案.

如图,连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
由旋转可知,AB=AD,∠DAB=60°,∠AED=90°,AE=DE=AC=BC=2,
∴△ABD为等边三角形,
∴AB=BD,
在△BAE与△BDE中,
∵AE=DE,BA=BD,BE=BE,
∴△BAE△BDE(SSS),
∴∠ABE=∠DBE,
根据等腰三角形“三线合一”可得BF⊥AD,且AF=DF,
∵AC=BC=2,∠ACB=90°,
∴AB=![]() ,
,
∴AB=BD=AD=![]() ,
,
∴AF=![]() ,
,
∴BF=![]() ,
,
∵∠AED=90°,AE=DE,
∴∠FAE=45°,
∵BF⊥AD,
∴∠FEA=45°,
∴EF=AF=![]() ,
,
∴BE=BFEF=![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D在AC上,DE⊥AB于点E,且CD=DE.点F在BC上,连接EF,AF,若∠CEF=45°,∠B=2∠CAF,BF=2,则AB的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(![]() ,4),B(3,m)是直线AB与反比例函数
,4),B(3,m)是直线AB与反比例函数![]() (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
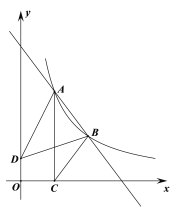
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
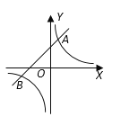
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
求:(1)反比例函数关系式;
(2)n的值;
(3)一次函数关系式;
(4)根据图像回答,当反比例函数的值大于一次函数的值时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织甲、乙两组同学参加国学经典知识对抗赛,每组有![]() 位选手,每场比赛两组各派
位选手,每场比赛两组各派![]() 人进行现场对抗比赛,满分为
人进行现场对抗比赛,满分为![]() 分,共进行了
分,共进行了![]() 场比赛.学校整理和汇总了这
场比赛.学校整理和汇总了这![]() 场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场比赛的成绩,并制成如下所示的尚不完整的统计表和图所示的折线统计图.
场次 | 一 | 二 | 三 | 四 | 五 | 六 |
甲组成绩 (单位:分) |
|
|
|
|
|
|
乙组成绩 (单位:分) |
|
|
|
|
|
|
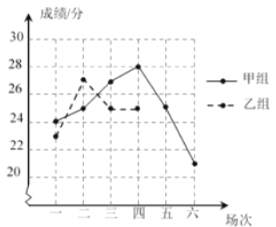
根据以上信息回答下面的问题:
(1)若甲、乙两组成绩的平均数相同,
①求![]() 的值;
的值;
②将折线统计图补充完整,并根据折线统计图判断哪组成绩比较稳定.
(2)若甲、乙两组成绩的中位数相等,直接写出![]() 的最小值.
的最小值.
(3)在(1)中的条件下,若从所有成绩为![]() 分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.
分的选手中随机抽取两人对其答题情况进行分析,请用列表法求抽到的两位选手均来自同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
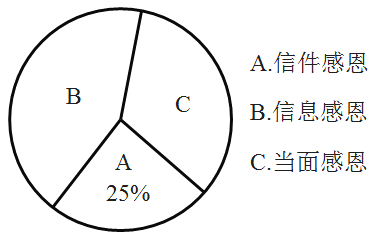
【题目】2019年9月10日是我国第35个教师节,某中学德育处发起了感恩小学恩师的活动,德育处要求每位同学从以下三种方式中选择一种方式表达感恩:A.信件感恩,B.信息感恩,C.当面感恩.为了解同学们选择以上三种感恩方式的情况,德育处随机对本校部分学生进行了调查,井根据调查结果绘制成了如下两幅不完整的统计图.

根据图中信息,解答下列问题:
(1)扇形统计图中C部分所对应的扇形圆心角的度数为________,并补全条形统计图;
(2)本次调查在选择A方式的学生中有两名男生和两名女生来自于同一所小学,德育处打算从他们四个人中选择两位在主题升旗仪式上发言,请用画树状图或列表的方法求恰好选到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,有下列结论:①
的图象如图所示,有下列结论:①![]() ;②
;②![]() ;③若
;③若![]() 为任意实数,则
为任意实数,则![]() ;④a-b+c>0;⑤若
;④a-b+c>0;⑤若![]() ,且
,且![]() ,则
,则![]() .其中,正确结论的个数为( )
.其中,正确结论的个数为( )
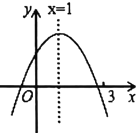
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数的百位上的数字减去十位上的数字等于其个位上的数字,则称这个三位数为“差数”,同时,如果百位上的数字为![]() 、十位上的数字为
、十位上的数字为![]() ,三位数
,三位数![]() 是“差数”,我们就记:
是“差数”,我们就记:![]() ,其中,
,其中,![]() ,
,![]() .例如三位数514.∵
.例如三位数514.∵![]() ,∴514是“差数”,∴
,∴514是“差数”,∴![]() .
.
(1)已知一个三位数![]() 的百位上的数字是6,若
的百位上的数字是6,若![]() 是“差数”,
是“差数”,![]() ,求
,求![]() 的值;
的值;
(2)求出小于300的所有“差数”的和,若这个和为![]() ,请判断
,请判断![]() 是不是“差数”,若是,请求出
是不是“差数”,若是,请求出![]() ;若不是,请说明理由.
;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com