
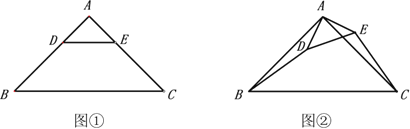
【题目】如图①,在等腰直角三角形中,![]() ,
,![]() ,D,E分别在
,D,E分别在![]() 上,且
上,且![]() ,此时有
,此时有![]() ,
,![]() .
.
(1)如图①中![]() 绕点A旋转至如图②时上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
绕点A旋转至如图②时上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(2)将图①中的![]() 绕点A旋转至DE与直线AC垂直,直线BD交CE于点F,若
绕点A旋转至DE与直线AC垂直,直线BD交CE于点F,若![]() ,
,![]() ,请画出图形,并求出BF的长.
,请画出图形,并求出BF的长.
【答案】(1)仍然成立;(2)画图见解析;![]() 长为
长为![]() 或
或![]() .
.
【解析】
(1)结论:BD=CE,BD⊥CE.如图1中,延长BD交CE的延长线于H.证明△BAD≌△CAE(SAS),即可解决问题;(2)分两种中情况分别求解①当逆时针旋转角度是45°时,②当逆时针旋转角度是225°时,先证明△ABD≌△ACE(SAS),从而求解DE,EC 的边长,再通过角的代换证明BF⊥EC,再证明Rt△DEF∽Rt△CEG,通过对应边成比例,求出FC的长度,最后再直角三角形△BCF用勾股定理求得BF的长度.
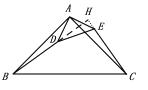
解:(1) 仍然成立
延长![]() 交于点
交于点![]() ,
,
![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]() ;
;
(2)如图,![]() 长为
长为![]() 或
或![]() ,
,
∵DE与直线AC垂直,
①当逆时针旋转角度是45°时,如图2:
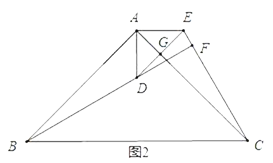
在△ABD和△ACE中,
AE=AD,∠BAD=∠CAE=45°,AB=AC,
∴△ABD≌△ACE(SAS)
∴BD=EC,
∵AB=20,AD=5![]() ,
,
∴AC=20,AE=5![]() ,
,
∵∠DAE=90°,
∴DE=10,
∵△AED是等腰直角三角形,
∴AG=GE=5,
∴GC=15,
在直角三角形GEC中,EC=5![]() ,
,
又∵∠ABD=∠ACE,∠BCA=45°,∠ABC=45°,
∴∠DBC+∠BCA+∠ACE=90°,
∴BF⊥EC,
∵∠EFD=∠EGC=90°,∠EDF=∠ECG,
∴Rt△DEF∽Rt△CEG,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() ,
,
∴FC=4![]() ,
,
在Rt△ABC中,BC=20![]() ,
,
在Rt△BCF中,BF=![]() ;
;
②当逆时针旋转角度是225°时,如图3,
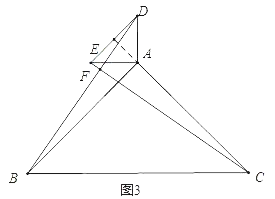
在△ABD和△ACE中,
AE=AD,BAD=∠CAE=45°,AB=AC,
∴△ABD≌△ACE(SAS)
∴BD=EC,
∵AB=20,AD=5![]() ,
,
∴AC=20,AE=5![]() ,
,
∵∠DAE=90°,
∴DE=10,
∵△AED是等腰直角三角形,
∴AG=GE=5,
∴GC=25,
在直角三角形GEC中,EC=5![]() ,
,
又∵∠ABD=∠ACE,∠ABC=45°,∠ACB=45°,
∴∠DBA+∠ABC+∠ACE=90°,
∴BF⊥EC,
∵∠EFD=∠EGC=90°,∠EDF=∠ECG,
∴Rt△DEF∽Rt△CEG,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() ,
,
∴FC=![]() ,
,
在Rt△ABC中,BC=20![]() ,
,
在Rt△BCF中,BF=![]() ;
;


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个类别,每位同学仅选一项.根据调査结果绘制了不完整的频数分布表和扇形统计图.
类别 | 频数(人数) | 频率 |
小说 | a | 0.5 |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | b | 1 |
根据图表提供的信息,回答下列问题:
(1)直接写出:a= .b= m= ;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请求选取的2人恰好是甲和乙的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在线段BD上,在BD的同侧作等腰Rt△ABC和等腰Rt△ADE,CD与BE、AE分别交于点P,M.对于下列结论:①△BAE∽△CAD;②MPMD=MAME;③2CB2=CPCM.其中正确的是( )

A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
如图①,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.

(1)请按要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′;
(2)在(1)所画图形中,∠AB′B=____.
(问题解决)
(3)如图②,在等边三角形ABC中,AC=7,点P在△ABC内,且∠APC=90°,∠BPC=120°,求△APC的面积.
小明同学通过观察、分析、思考,对上述问题形成了如下想法:
想法一:将△APC绕点A按顺时针方向旋转60°,得到△AP′B,连接PP′,寻找PA,PB,PC三条线段之间的数量关系;
想法二:将△APB绕点A按逆时针方向旋转60°,得到△AP′C′,连接PP′,寻找PA,PB,PC三条线段之间的数量关系.…
请参考小明同学的想法,完成该问题的解答过程.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为DC的中点,AD:AB=![]() :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正确的是( )
;④EFEP=4AOPO.其中正确的是( )
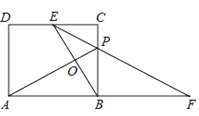
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,∠AEF的角平分线交AB于点M,∠EFC的角平分线交CD于点N,连接MF、NE.
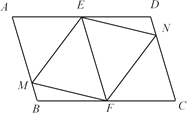
(1)求证:四边形EMFN是平行四边形.
(2)小明在完成(1)的证明后继续进行了探索,他猜想:当AB=AD时,四边形EMFN是矩形.请在下列框图中补全他的证明思路.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com