
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,∠AEF的角平分线交AB于点M,∠EFC的角平分线交CD于点N,连接MF、NE.
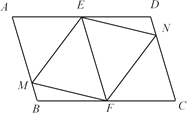
(1)求证:四边形EMFN是平行四边形.
(2)小明在完成(1)的证明后继续进行了探索,他猜想:当AB=AD时,四边形EMFN是矩形.请在下列框图中补全他的证明思路.

【答案】(1)见解析;(2)∠EFM=∠BMF,AM=BM(或:M是AB中点).
【解析】
(1)根据平行四边形的性质可得∠A=∠C,∠AEF=∠CFE,AD=BC,根据角平分线的定义和中点的定义可得∠AEM=∠CFN,AE=CF,利用ASA即可证明△AME≌△CNF,可得EM=FN,∠FEM=∠FEN,根据内错角相等可得EM//FN,即可证明四边形EMFN是平行四边形;(2)由AE=BF,AE//BF可得四边形ABFE是平行四边形,可得EF//AB,可得∠MEF=∠AME,∠EFM=∠BMF,由角平分线可得∠AEM=∠MEF,即可证明∠AEM=∠AME,可得AE=AM,由AB=AD可得M为AB中点,即可证明BM=BF,进而可得∠BMF=∠BFM,即可证明∠BFM=∠EFM,可得∠EFM+∠EFN=90°,可得四边形EMFN是矩形.
(1)在□ABCD中,∠A=∠C,AD∥BC,AD=BC
∵E、F分别是AD、BC的中点,
∴AE=![]() AD,CF=
AD,CF=![]() BC,
BC,
又∵AD=BC,
∴AE=CF,
∵AD∥BC,
∴∠AEF=∠CFE,
∵EM平分∠AEF,FN平分∠EFC,
∴∠AEM=∠FEM=![]() ∠AEF,∠CFN=∠FEN=
∠AEF,∠CFN=∠FEN=![]() ∠CFE,
∠CFE,
∵∠AEF=∠CFE,∠AEM=![]() ∠AEF,∠CFN=
∠AEF,∠CFN=![]() ∠CFE,
∠CFE,
∴∠AEM=∠CFN,
在△AME和△CNF中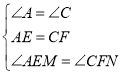 ,
,
∴△AME≌△CNF(ASA),
∵∠FEM=∠FEN,
∴EM∥FN,
∵△AME≌△CNF,
∴EM=FN,
∵EM∥FN,EM=FN,
∴四边形EMFN是平行四边形.
(2)∵AE=BF,AE//BF,
∴四边形ABFE是平行四边形,
∴AB//EF,
∴∠MEF=∠AME,∠EFM=∠BMF,
∵∠AEM=∠MEF,
∴∠AEM=∠AME,
∴AE=AM,
∵E为AD中点,AB=AD,
∴M为AB中点,即AM=BM,
∵AE=BF,
∴BM=BF,
∴∠BMF=∠BFM,
∴∠BFM=∠EFM,
∵∠EFN=∠CFN,
∴∠EFM+∠EFN=90°,即∠MFN=90°,
∴四边形EMFN是矩形.
故答案为:∠EFM=∠BMF,AM=BM(或:M是AB中点).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
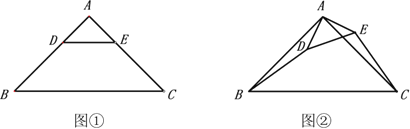
【题目】如图①,在等腰直角三角形中,![]() ,
,![]() ,D,E分别在
,D,E分别在![]() 上,且
上,且![]() ,此时有
,此时有![]() ,
,![]() .
.
(1)如图①中![]() 绕点A旋转至如图②时上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
绕点A旋转至如图②时上述结论是否仍然成立?若成立,请证明;若不成立,请说明理由.
(2)将图①中的![]() 绕点A旋转至DE与直线AC垂直,直线BD交CE于点F,若
绕点A旋转至DE与直线AC垂直,直线BD交CE于点F,若![]() ,
,![]() ,请画出图形,并求出BF的长.
,请画出图形,并求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,支付方式的“众数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校1200名学生发起向贫困山区学生捐款活动,为了解捐款情况,学生会随机抽取了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②.
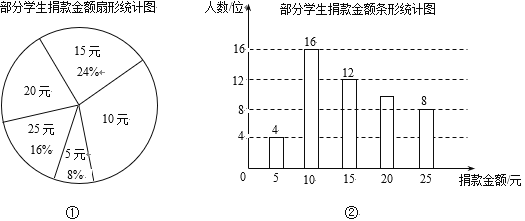
请根据以上信息,解答下列问题:
(1)本次抽样调查的样本容量为____;
(2)图①中“20元”对应扇形的圆心角的度数为_____°;
(3)估计该校本次活动捐款金额为15元以上(含15元)的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“大美湿地,水韵盐城”.某校数学兴趣小组就“最想去的盐城市旅游景点”随机调查了本校部分学生,要求每位同学选择且只能选择一个最想去的景点,下面是根据调查结果进行数据整理后绘制出的不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)求被调查的学生总人数;
(2)补全条形统计图,并求扇形统计图中表示“最想去景点D”的扇形圆心角的度数;
(3)若该校共有800名学生,请估计“最想去景点B“的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
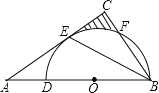
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA=![]() ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月1日是儿童节,为了迎接儿童节的到来,兰州某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于24件,并且商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
(3)在(2)条件下,若每件甲种玩具售价30元,每件乙种玩具售价45元,请求出卖完这批玩具获利W(元)与甲种玩具进货量m(件)之间的函数关系式,并求出最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com