
【题目】如图,在△ABC中,BE是它的角平分线,∠C=90°,D在AB边上,以DB为直径的半圆O经过点E,交BC于点F.
(1)求证:AC是⊙O的切线;
(2)已知sinA=![]() ,⊙O的半径为4,求图中阴影部分的面积.
,⊙O的半径为4,求图中阴影部分的面积.
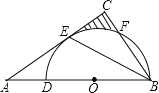
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OE.根据OB=OE得到∠OBE=∠OEB,然后再根据BE是△ABC的角平分线得到∠OEB=∠EBC,从而判定OE∥BC,最后根据∠C=90°得到∠AEO=∠C=90°证得结论AC是⊙O的切线.
(2)连接OF,利用S阴影部分=S梯形OECF-S扇形EOF求解即可.
解:(1)连接OE.
∵OB=OE
∴∠OBE=∠OEB
∵BE是∠ABC的角平分线
∴∠OBE=∠EBC
∴∠OEB=∠EBC
∴OE∥BC
∵∠C=90°
∴∠AEO=∠C=90°
∴AC是⊙O的切线;
(2)连接OF.
∵sinA=![]() ,∴∠A=30°
,∴∠A=30°
∵⊙O的半径为4,∴AO=2OE=8,
∴AE=![]() ,∠AOE=60°,∴AB=12,
,∠AOE=60°,∴AB=12,
∴BC=![]() AB=6,AC=6
AB=6,AC=6![]() ,
,
∴CE=AC﹣AE=2![]() .
.
∵OB=OF,∠ABC=60°,
∴△OBF是正三角形.
∴∠FOB=60°,CF=6﹣4=2,∴∠EOF=60°.
∴S梯形OECF=![]() (2+4)×2
(2+4)×2![]() =6
=6![]() .
.
S扇形EOF=![]() ,
,
∴S阴影部分=S梯形OECF﹣S扇形EOF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E为DC的中点,AD:AB=![]() :2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②
:2,CP:BP=1:2,连接EP并延长,交AB的延长线于点F,AP、BE相交于点O.下列结论:①EP平分∠CEB;②![]() =PBEF;③PFEF=2
=PBEF;③PFEF=2![]() ;④EFEP=4AOPO.其中正确的是( )
;④EFEP=4AOPO.其中正确的是( )
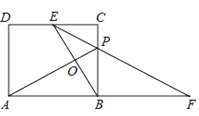
A. ①②③B. ①②④C. ①③④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E、F分别是AD、BC的中点,∠AEF的角平分线交AB于点M,∠EFC的角平分线交CD于点N,连接MF、NE.
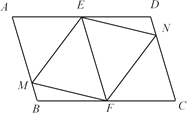
(1)求证:四边形EMFN是平行四边形.
(2)小明在完成(1)的证明后继续进行了探索,他猜想:当AB=AD时,四边形EMFN是矩形.请在下列框图中补全他的证明思路.

查看答案和解析>>
科目:初中数学 来源: 题型:
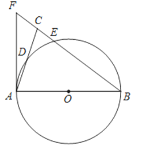
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,BC的延长线与⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE,AF的长.
,CE:EB=1:4,求CE,AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
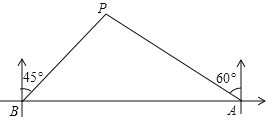
【题目】如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+k+3=0有两个不相等的实数根
(1)求k的取值范围;
(2)若k为大于3的整数,且该方程的根都是整数,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
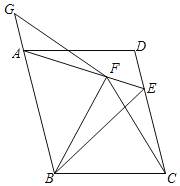
【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.
(1)如图①,AB是直径,要使EF是⊙O的切线,还须添加一个条件是(只需写出三种情况).
(ī) (īī) (īīī)
(2)如图(2),若AB为非直径的弦,∠CAE=∠B,则EF是⊙O的切线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
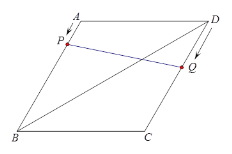
【题目】如图,在菱形ABCD中,已知∠BAD=120°,对角线BD长为12.
(1)求菱形ABCD的周长;
(2)动点P从点A出发,沿A→B的方向,以每秒1个单位的速度向点B运动;在点P出发的同时,动点Q从点D出发,沿D→C→B的方向,以每秒2个单位的速度向点B运动.设运动时间为t(s).
①当PQ恰好被BD平分时,试求t的值;
②连接AQ,试求:在整个运动过程中,当t取怎样的值时,△APQ恰好是一个直角三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com