


科目:初中数学 来源: 题型:
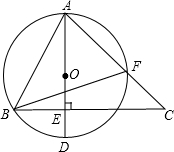 如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.
如图,AD是⊙O的直径,AB、AF是弦,BE⊥AD与AF的延长线交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:
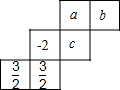 如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件:
如图,是一个正方体纸盒的表面展开图,在其中的三个正方形a,b,c 内分别填入适当的数,使得折成正方体后相对的面上的两个数满足下列条件:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
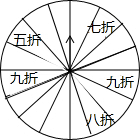 某酒店为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘等分成16份),并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会;如果转盘停止后,指针正好对准九折、八折、七折或五折区域,顾客就可以获得此项待遇.
某酒店为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘等分成16份),并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会;如果转盘停止后,指针正好对准九折、八折、七折或五折区域,顾客就可以获得此项待遇.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com