
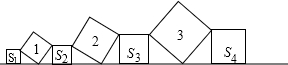
 如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )
如图,直线l上依次摆放着一系列正方形,斜放置的正方形面积分别为1,2,3,…,n,正放置的正方形面积分别为S1,S2,S3,…,Sn,当n=100时,则S1+S2+S3+…+S100等于( )| A. | 2500 | B. | 2550 | C. | 2600 | D. | 2800 |
分析 如图1,根据正方形的性质得AC=CD,∠ACD=90°,再根据等角的余角线段得∠BAC=∠DCE,则可根据“AAS”判定△ACB≌△DCE,得到AB=CE,BC=DE;由勾股定理得AC2=AB2+BC2=AB2+DE2,即Sb=Sa+Sc=5;如图2,由前面的结论可得S1+S2=1=1+2×0=1,S3+S4=3=1+2×1=3,S5+S6=1+2×2=5,…S99+S100=99,然后相加得到S1+S2+S3+…+S100=2500.
解答 解:如图1,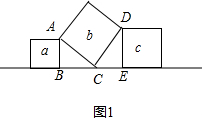 ∵a、b、c都是正方形,
∵a、b、c都是正方形,
∴AC=CD,∠ACD=90°,
∴∠ACB+∠DCE=90°,
而∠ACB+∠BAC=90°,
∴∠BAC=∠DCE,
在△ACB和△DCE中,
$\left\{\begin{array}{l}{∠ABC=∠CED}\\{∠BAC=∠DCE}\\{AC=CD}\end{array}\right.$,
∴△ACB≌△DCE(AAS),
∴AB=CE,BC=DE;
在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=AB2+DE2,
即Sb=Sa+Sc=1+4=5;
如图2,由前面的结论可得S1+S2=1=1+2×0=1,
S3+S4=3=1+2×1=3,
S5+S6=1+2×2=5,
…
S99+S100=99,
∴S1+S2+S3+…+S100=1+3+5+…+99=2500.
故选:A.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了勾股定理和正方形的性质.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:选择题
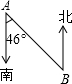 石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )
石家庄现在正在修建的地铁1号线大致是东西走向的,已知在白佛站往东有一个拐弯,现记弯道的两个端点分别为A,B,如图所示,若在A地测得地铁隧道的走向是南偏东46°,则为了使地铁隧道能够准确接通,在B地施工的地铁隧道的走向应为( )| A. | 北偏西46° | B. | 北偏西44° | C. | 南偏东46° | D. | 南偏西44° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com