
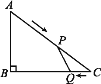
【题目】如图,在![]() 中,
中,![]() ,
,![]() 米,
米,![]() 米,动点
米,动点![]() 以
以![]() 米/秒的速度从点
米/秒的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 移动.同时,动点
移动.同时,动点![]() 以
以![]() 米/秒的速度从点
米/秒的速度从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 移动.当其中有一点到达终点时,另一点也随之停止移动.设移动的时间为
移动.当其中有一点到达终点时,另一点也随之停止移动.设移动的时间为![]() 秒.
秒.
(1)①当![]() 秒时,求
秒时,求![]() 的面积;
的面积;
②求![]() 的面积
的面积![]() (米
(米![]() )关于时间
)关于时间![]() (秒)的函数表达式.
(秒)的函数表达式.
(2)在点![]() 移动的过程中,当
移动的过程中,当![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
【答案】(1)①![]() 米
米![]() ,②
,②![]() (
(![]() );(2)当
);(2)当![]() 的值为
的值为![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.
【解析】
(1)①作PD⊥BC于D,利用三角形中位线定理即可求得PD的长,然后利用三角形的面积公式即可求解.
②作QE⊥PC于点E,利用Rt△QEC∽Rt△ABC求出QE即可.
(3)三种情况进行讨论①PC=QC ②PQ=QC ③PC=PQ,分别列出方程即可解决.
在![]() 中,
中,![]() 米,
米,![]() 米,
米,![]() 米.
米.
由题意,得![]() 米,
米,![]() 米,则
米,则![]() 米.
米.
(1)①如图(a),过点![]() 作
作![]() 于点
于点![]() .
.
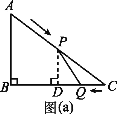
当![]() 秒时,
秒时,![]() (米),
(米),![]() 米,
米,
易知![]() 为
为![]() 的中位线,
的中位线,
![]() 米,
米,
![]()
![]() (米
(米![]() ).
).
②如图(b),过点![]() 作
作![]() 于点
于点![]() ,
,
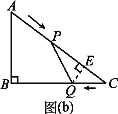
则![]() ,
,![]() ,
,![]() 米.
米.
![]()
![]() (
(![]() ).
).
(2)当![]() 时,由
时,由![]() 米,
米,![]() 米,
米,
得![]() ,解得
,解得![]() ;
;
当![]() 时,如图(c),过点
时,如图(c),过点![]() 作
作![]() ,
,
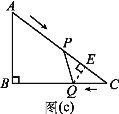
则![]() 米,
米,![]() 米,可证
米,可证![]() ,
,
故![]() ,即
,即![]() ,解得
,解得![]() ;
;
当![]() 时,如图(d),过点
时,如图(d),过点![]() 作
作![]() ,
,
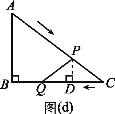
则![]() 米,
米,![]() 米,可证
米,可证![]() ,
,
故![]() ,即
,即![]() ,解得
,解得![]() .
.
故当![]() 的值为
的值为![]() 或
或![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的内接三角形,AB为⊙O直径,AB=12,AD平分∠BAC,交BC于点 E,交⊙O于点D,连接BD.
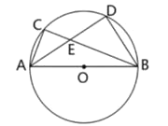
(1)求证:∠BAD=∠CBD;
(2)若∠AEB=125°,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列一元二次方程
(1) (2x-1)2=25
(2) 3x2-6x-1=0
(3) x2-4x-396=0
(4) (2-3x)+(3x-2)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C,E,A在同一直线上,D,E,B在同一直线上,测得A处与E处的距离为80 m,C处与D处的距离为34 m,∠C=90°,∠ABE=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7)
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为弧BF上一点,且BE=CF,
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=8,求AC的长.
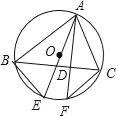
查看答案和解析>>
科目:初中数学 来源: 题型:
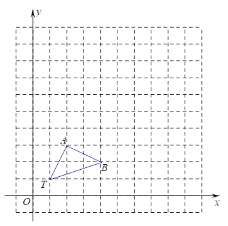
【题目】如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
(1)以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 ,点B′的坐标为
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,AC是⊙O的弦,过点C作CE⊥AB于点D,交⊙O于点E,过点B作BF⊥AC于点F,交CE于点G,连接BE。

(1)求证:BE=BG;
(2)过点B作BH⊥AB交⊙O于点H,若BE的长等于半径,BH=4,AC=![]() ,求CE的长。
,求CE的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com