
【题目】如图,直线AB、CD相交于点O,OM⊥AB.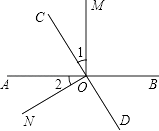
(1)若∠1=∠2,求∠NOD.
(2)若∠1= ![]() ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.
【答案】
(1)解:∵OM⊥AB,
∴∠AOM=∠1+∠AOC=90°,
∵∠1=∠2,
∴∠NOC=∠2+∠AOC=90°,
∴∠NOD=180°﹣∠NOC=180°﹣90°=90°;
(2)解:∵OM⊥AB,
∴∠AOM=∠BOM=90°,
∵∠1= ![]() ∠BOC,
∠BOC,
∴∠BOC=∠1+90°=3∠1,
解得∠1=45°,
∠AOC=90°﹣∠1=90°﹣45°=45°,
∠MOD=180°﹣∠1=180°﹣45°=135°.
【解析】根据垂线的定义,角的运算,掌握图形间角的关系得出答案.
【考点精析】本题主要考查了对顶角和邻补角和垂线的性质的相关知识点,需要掌握两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( ) 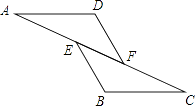
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
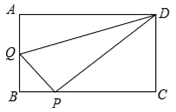
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
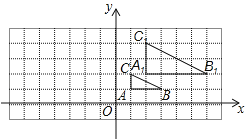
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛的积分规则:胜一场得3分,平一场得1分,负一场得0分.一个队进行了14场比赛,其中负5场,共得19分,那么这个对共胜了( )场.
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰兴市新区对曾涛路进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.则原有树苗( )棵.
A.100
B.105
C.106
D.111
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com